Transformer Model

• The transformer ¹ model makes use of the Attention mechanism to transform an input sequence to another output sequence.

Transformer Model. Image taken from Zhang et al.

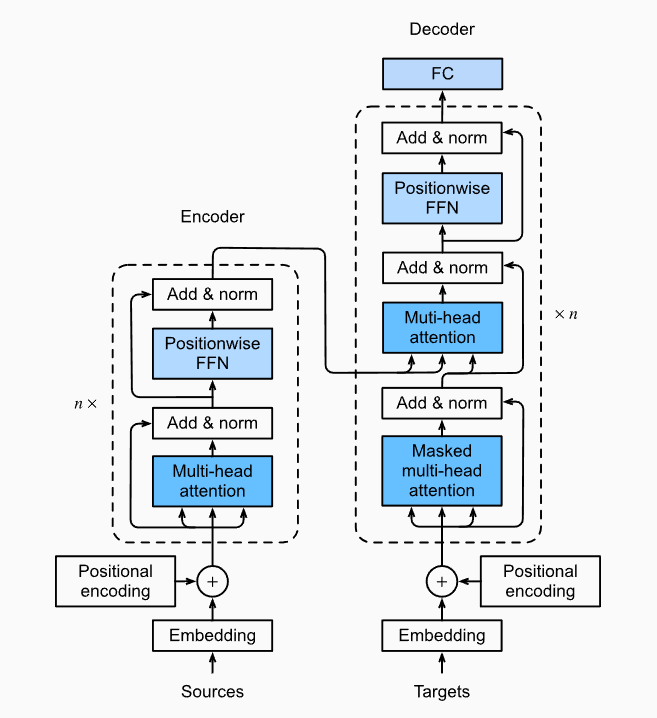
Architecture §

• The model takes in an embedding (from some tokenizer or byte pair encoding) that acts as a more compact representation of the input data.

  • The embedding is obtained using an embedding matrix .
  • To obtain tokens, we also use an unembedding matrix . By convention we use weight tying so that

• The model first performs positional encoding to represent the position of a token in the sequence.

• The model then consists of an encoder and a decoder

  • The encoder takes in the input sequence and outputs a latent space representation called a context variable for each position in the input sequence.
    • Encoders can attend to the whole sequence as needed.
    • The context variables integrate the meaning of potentially helpful tokens within context.
  • The decoder takes in the context variable as well as another sequence and produces an output sequence.
    • The architecture for a decoder is mostly similar to the encoder except for the presence of a specialized layer.
    • It makes use of encoder-decoder-attention which performs attention such that the queries are from the previous decoder layer, and they keys and values are from the encoder outputs.
    • Decoders can only attend to the tokens that have already been generated.
    • In deployment, the decoder is simply fed the outputs it has generated so far.
  • The encoder produces the retrieval system for one language and the decoder produces the queries from another language. Queries, Keys and Values are all calculated by the model.

• To utilize the attention mechanism, transformers make use of weight matrices for query, key and value respectively. These allow us to learn QKV representations of the input vector

• Transformers make use of residual connections between the previous input and the output. We also make use of layer normalization.

  • This is done as attention can be used to move information between tokens via residual connections. Effectively, we are updating the output repeatedly.

• Parallelizing a transformer model necessitates using the matrix ( = no. of tokens and the embedding dimension) containing the embeddings of each token in the sequence. We can then get the key, query and value vectors for each token using matrix multiplication

  We compute the attention matrix using the scaled dot product can then be done using

  The output can be obtained by computing

  And masking can be further done using the masking matrix

  • For completeness we note that , , . We always have .
  • By convention, we often have .

• To obtain the output, we make sure to multiply with a matrix that will reshape the matrices to the correct dimensions after passing through all heads. The output is obtained via matrix multiplication

Topics §

• Positional Encoding
• Extending Context in Transformers
• Adaptive Transformer
• Sparsity in Transformer

Remarks §

• The encoder and decoder need not be used together. They can be taken and trained separately.

  • Encoder-Only Transformers are best suited for tasks where there is a need to understand the full sequence within one language.
    • They are pre-trained by corrupting the given sequence and tasking the model with reconstructing the initial sequence.
  • Decoder-Only Transformers are best suited for tasks that involve text-generation.
    • They are pre-trained by predicting the next word of the sequence.

• Transformers scale very well with increased model size and training computation.

  • This scaling follows a power law.
  • This scaling is due to the fact the transformer is also easily parallelizable, enabling deeper architectures without performance loss.
    • Attention is parallelizable because the computation for each token is independent

Extensions §

• ² applies NAS to search for a better alternative to the transformer.
  • We use tournament selection architecture search warm started with the Transformer model.
  • We make use of a Genetic Algorithm based approach to evolve the architecture.
    • Assuming no model overfits during its training, which is what we observed in our experiments, and that its fitness monotonically increases with respect to the number of train steps it is allocated, a comparison between two child models can be viewed as a comparison between their fitnesses at the lower of the two’s cumulative train steps.
  • We make use of Progressive Dynamic Hurdles (PDH) to allow models that are consistently performing well to train for more steps.
    • Rationale: This gives a signal for how the child model would perform on the dataset .
    • After a predetermined number of child models have been evaluated, a hurdle is created using the mean fitness of the current population.
    • The child models with fitness above train an additional number of steps.
    • In this way poor performing models do not consume as many resources when their fitness is computed.
  • The search space incorporates both convolutions and attention layers.
    • We have two stackable cells — one for encoders and one for decoder.

Progressive Dynamic Hurdles. Image taken from So, Liang, Le (2019)

Evolved Transformer Encoder blocks. Image taken from So, Liang, and Le (2019)

Evolved Transformer Decoder block. Image taken from So, Liang, and Le (2019)

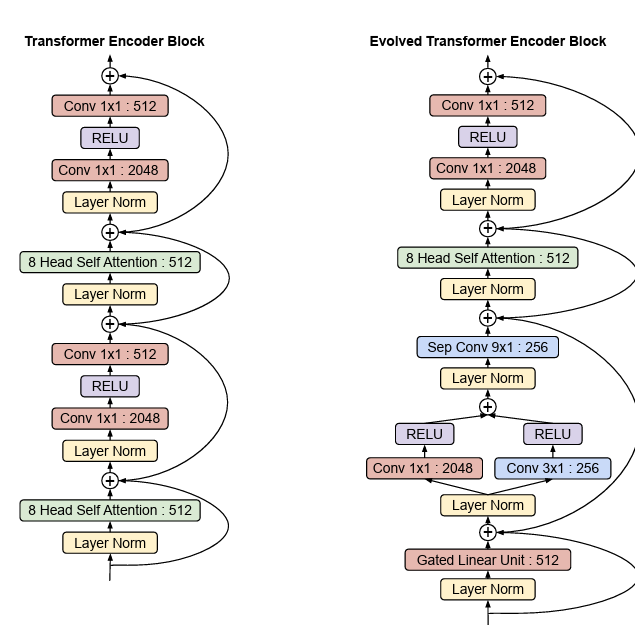
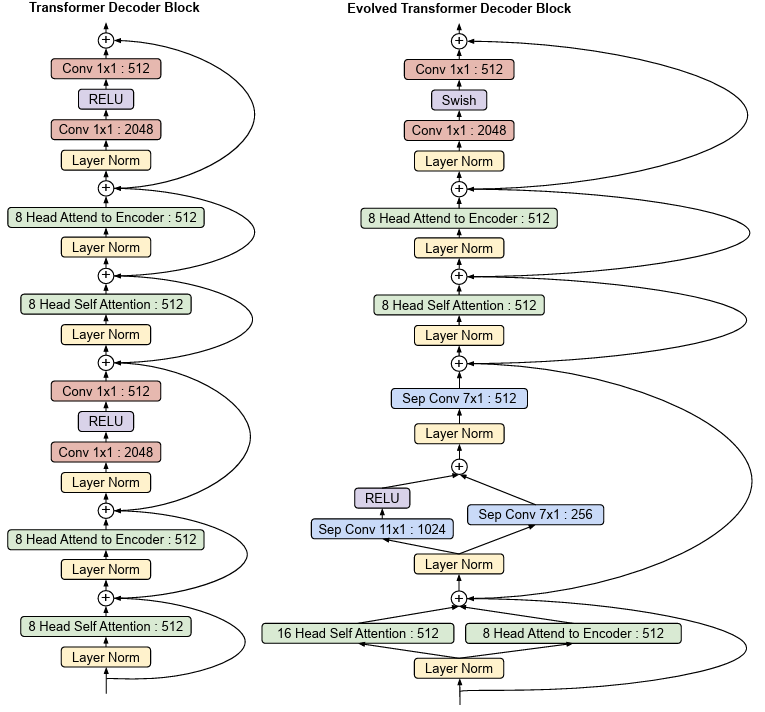
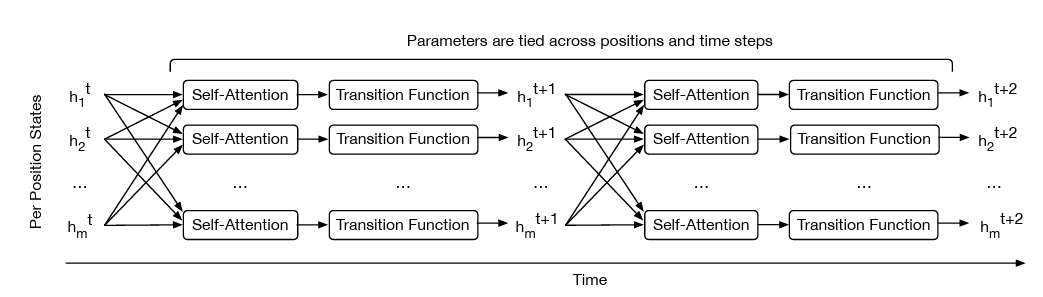
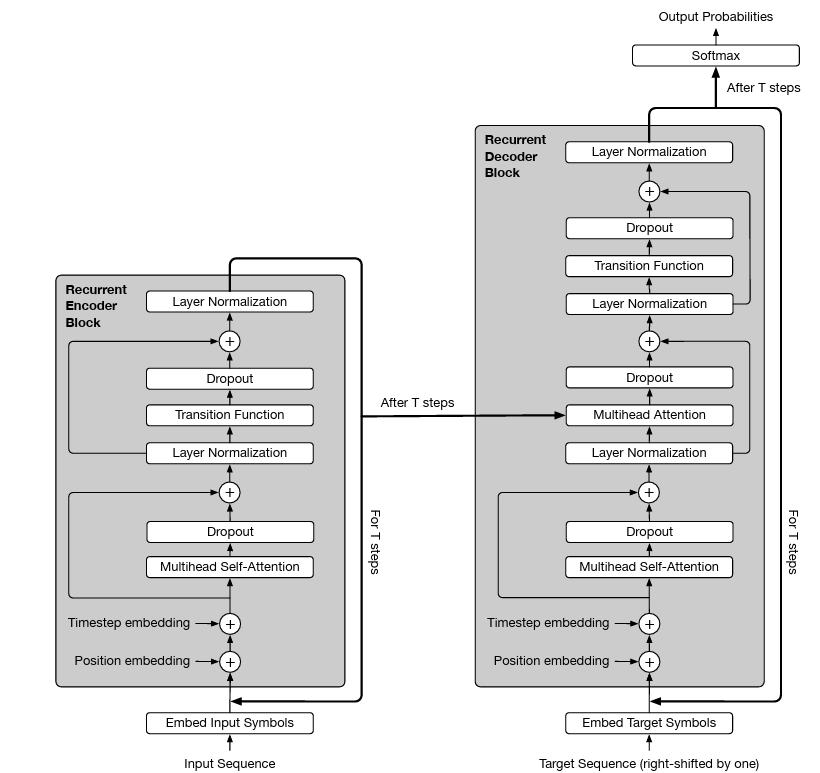
• ³ introduces the Universal Transformer (UT) - a parallel-in-time self-attentive recurrent sequence model which combines the transformer architecture with the inductive bias of RNNs towards learning iterative or recursive transformations.

  • It allows for better generalization for a transformer since the inductive bias of an RNN may be crucial for various tasks.

  • In each recurrent step, the UT iteratively refines its representations for all symbols in the sequence in parallel using a self-attention mechanism

  • The Universal Transformer follows the usual Encoder-Decoder architecture. Both encoder and decoder are RNNs.

    • The recurrent networks in the Universal Transformer recur over consecutive revisions of the vector representations of each position.
    • In each recurrent time step, each representation is revised in two steps:

      • Self-attention exchanges information across all positions.

      • Apply a transition function to the outputs independently. This is applied as follows

        Where is the sinusoidal positional encoding matrix but with an additional time dimension

  • Our choices for transition functions are:

    • A separable convolution
    • A fully connected neural network with a single ReLU between two affine transformations, applied to each row of .

  • We also make use of a dynamic Adaptive Computation Time (ACT) mechanism to dynamically control the number of computational steps to process each input symbol.

    Once the per-symbol recurrent block halts, its state is copied to the next step until all blocks halt.

  • As the per-symbol recurrent transition function can be applied any number of times, UT is a block of parallel RNNs, one for each symbol, with shared parameters, evolving per-symbol hidden states concurrently, generated at each step by attending to the sequence of hidden states at the previous step.

  • With sufficient memory, the Universal Transformer can be shown to be Turing Complete.

    • Unlike an RNN, UTs can access memory in recurrent steps.

Universal Transformer. Image taken from Deghani et al. (2019)

Universal Transformer Block. Image taken from Deghani et al. (2019)

Links §

• Zhang et. al Ch. 11 - for everything about the basics of the transformer model.

• All about Attention - more about attention

• The Transformer Family v2.0 by Lilian Weng

Footnotes §

1. Vaswani et al. (2017) Attention is All You Need ↩

2. So, Liang, and Le (2019) The Evolved Transformer ↩

3. Deghani et al. (2019) Universal Transformers ↩