Positional Encoding

• Positional Encoding is done to account for the fact the order tokens appear in sequence is important

  • The original positional encoding proposed encodes both the absolute position of a token, and its position relative to other tokens. For any fixed offset , the positional encoding at can be obtained through linear projection of at .
  • An ideal positional encoding has the following properties ¹
    • Unique encoding for each position across sequences regardless of sequence length.
    • Linear relation between two encoded positions (for simplicity).
    • Generalizable to longer sequences than those encountered in training.
    • Deterministically generated
    • Extensible to multiple dimensions.

• Position encoding can either be applied to only the first input, or in every layer. The latter tends to be more performance.

• The positional encoding is applied to as follows

• Sinusoidal Positional Embedding constructs the embedding as follows

• Learned Positional Encoding involves treating as a trainable matrix. We can treat layers as having shared or independent positional encoding matrices.

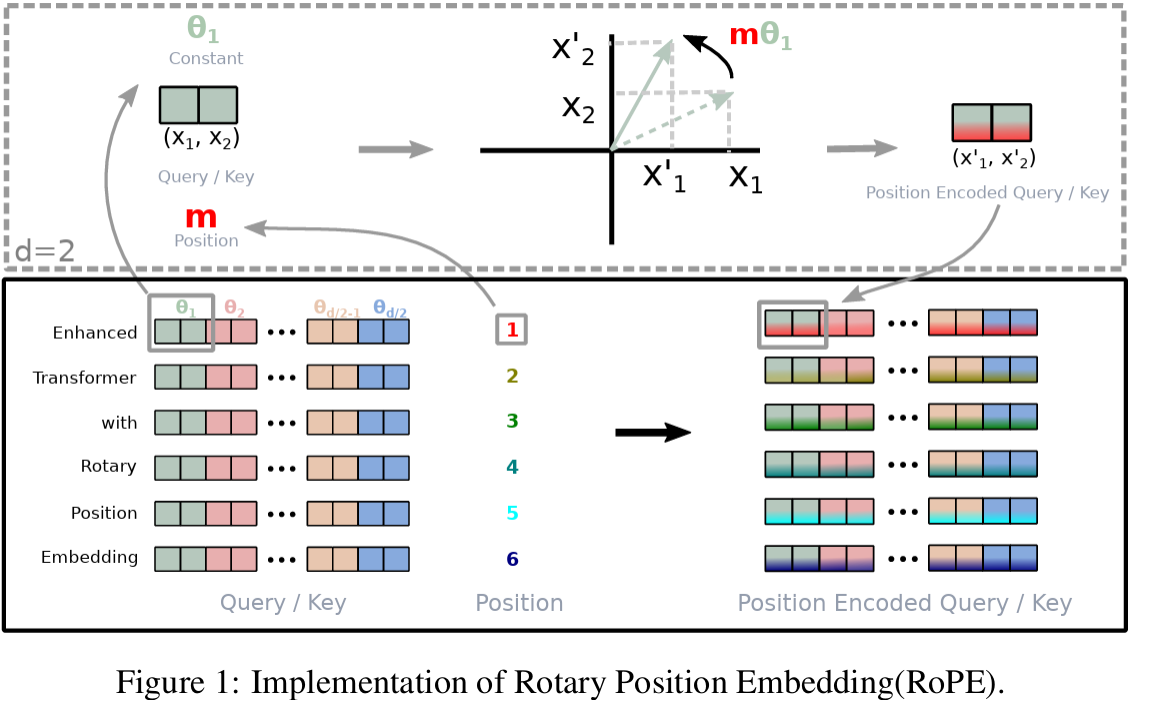
• Rotary Position Embedding (RoPE) ² encodes the absolute position with a rotation matrix while incorporating explicit relative position dependency.

  • We formulate the inner product of and such that it is a function only dependent on the word embeddings and the relative distance . Thus

  • Consider the simpler case of dimensional embeddings. By our stipulation

    Further assume we have the initial conditions with no position information encoded.

    We use Complex numbers to represent the vectors. Let and denote the radial and angular components of . Then we note that we can rewrite . Applying this to and we get the relations

    Where and .

    We can find a solution by setting . This gives us

    One solution could therefore be to set and . Thus the radial functions are independent from position.

    Furthermore, since the angular functions do not depend on the query and the key so we simply set . We have

    For some function .

    Also setting

    Thus must be linear. Using , and .

    Let us set , and . The final solution is

    Therefore

    Where denotes complex conjugation. .

  • We can represent the solution using a rotation matrix of the form

  • In the general form where , where is even. We divide the space into subspaces and by linearity, (for both and ) is of the form

    Where

    And

    The inner product is therefore

  • For completeness, set . Intuitively tokens do not influence other tokens that are relatively far away.

  • Because is sparse, we can perform multiplication with it uses the Hadamard product as follows

  • Notice we do not add position information to the values.

  • One main challenge with RoPE is extrapolation.

Rotary Position Embedding. Image taken from Su et al. (2021)

• ³ proposes a modified relative positional encoding for use in models that have extended context lengths.

  We use the following decomposition. Let be the -th row of .

  We perform the following reparameterization

  • Replace with where corresponds to the sinusoidal position embedding. Only the relative distance matters for where to attend
  • Replace with trainable parameters for and corresponding to content and location respectively.
    • Since the query vector is the same for all query positions, the bias should remain the same regardless of query positions.
  • Split to and for content and local information.
  • The final reparameterization now looks like
    • The first term corresponds to content-based addressing
    • The second term corresponds to content-dependent positional bias.
    • The third term corresponds to global content bias
    • The fourth term correspond to global positional bias

• ⁴ introduces relative positional encoding.
  • Rationale: This is one approach to consider arbitrary pairwise relations between any two input tokens. We treat the input as a labeled fully connected digraph.
  • The edge between input elements is represented by the vectors . We apply the positional embedding by modifying the key-value matrices
  • We clip the maximum distance to a maximum absolute value

    • Rationale: This lets us generalize to sequence lengths not seen in training. Also it is hypothesized that previse positional information is not useful beyond a certain distance.

    • We consider edge labels (within the interval ). We then obtain

      Where .

      and are then treated as learnable training parameters.

    • For efficiency, we share the relative position encoding either across heads or across sequences

  • When computing the scaled dot product, we separate the computation and perform tensor reshaping on the second term in the following
    The computation for the output using is done similarly, separating and and reshaping the term corresponding to .

Incorporating Long Contexts §

• Attention with Linear Biases (ALiBi) ⁵ proposes a position encoding method where we add a bias for query-key attention scores with a penalty proportional to their distance.

  • The authors speculate that the failure to extrapolate is due to the choice of positional encoding used.

  • Using ALiBi entails training the model on short sequences. Thus, training incurs lower cost.

  • ALiBi simply entails modifying the attention mechanism by introducing a static, non-learned bias. For the -th query, we perform

    Where is a head specific sloping parameter.

    • The paper uses a geometric sequence for . So for heads we have

  • ALiBi has an inductive bias towards recency. The penalty decreases as the distance between a key and query diminishes.

  • ALiBi’s decrease in perplexity when given longer sequences is largely explained by its improved avoidance of the early token curse

  • Limitation: When using a larger context during validation, ALiBi might not actually be using contexts longer than the one it was trained on.

• ⁶ propose the DA-Transformer (distance aware transformer) which incorporates the real distance between tokens in re-scaling raw self-attention weights.
  • Rationale: Global and local context modelling usually have different distance preferences for attention.
  • In each attention head, we use a learnable parameter to weight the relative distance. Let be the relative distance matrix where then
    It is stipulated that being more positive favors long-distance information, while it being more negative favors short-term context.
  • We then design a function to obtain the rescaled coefficients . The function satisfies.
    • since zero distance does not influence attention weights.
    • . If attention prefers local information, the long-distance information should be surpassed.
    • . We introduce this bound so that the model can process long sequences without over-emphasizing distance contexts.
    • The scale of is tunable to adjust the intensity of distance information.
    • is monotone.
  • Our choice for is a learnable sigmoid function
    Where is a head-specific learnable parameter.
  • The re-scaled coefficients are used to adjust the attention weights. We obtain the attention matrix as follows
    • The scaling is multiplicative since adding might over-amplify the attention weights.
    • The ReLU is incorporated since the sign of can be both positive and negative. Thus, multiplication does not reflect distance information.
    • ReLU also adds sparsity since only positive attention is amplified.
  • The extra time and space complexity for computing the above is and respectively.

Links §

• Zhang et. al Ch. 11 - for everything about the basics of the transformer model.

• All about Attention - more about attention

• The Transformer Family v2.0 by Lilian Weng

• Transformer Model

Footnotes §

1. RoPE has all these properties. See https://huggingface.co/blog/designing-positional-encoding ↩

2. Su et al. (2021) RoFormer: Enhanced Transformer with Rotary Position Embedding ↩

3. : Dai et al. (2019) Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context ↩

4. Shaw, Uszkoreit, Vaswani (2018) Self-Attention with Relative Position Representations ↩

5. Press, Smith, Lewis (2021) Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation ↩

6. Wu, Wu, Huang (2021) DA-transformer: Distance Aware Transformer ↩