Sparsity in Transformer

• A simple approach to sparsity is to restrict the attention span of each token to local context only.

• ¹ introduces Sparse Transformers via a sparse factorization of the transformer that scales as .

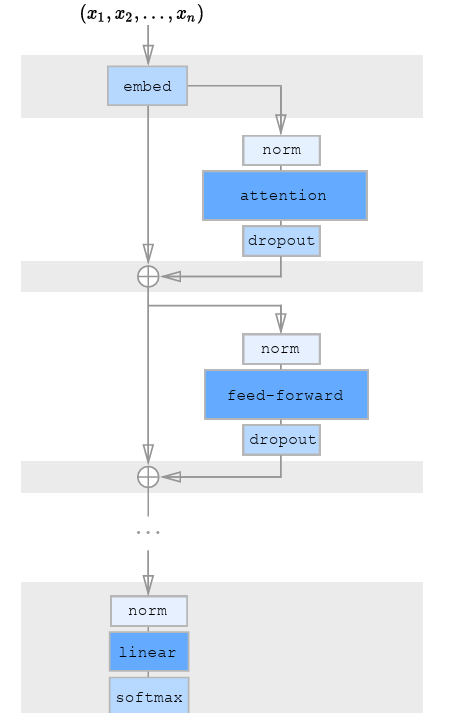
  • We also improve training using a structured residual block and weight initialization scheme.

  • We introduce sparse attention kernels that can efficiently compute subsets of the attention matrix.

  • We reduce memory usage during training by recomputing attention weights.

  • The key motivation behind factorization is the insight that most layers have sparse attention patterns across most data points.

  • Factorized self attention has attention heads where the -th head define a subset of indices. which determines the connectivity pattern — that is, where the -th output vector attends to.

    Here, .

    • For every pair, we set such that can attend to through a path of locations with maximum length . Each location .

      This allows us to propagate signals throughout the sequence while reducing computation

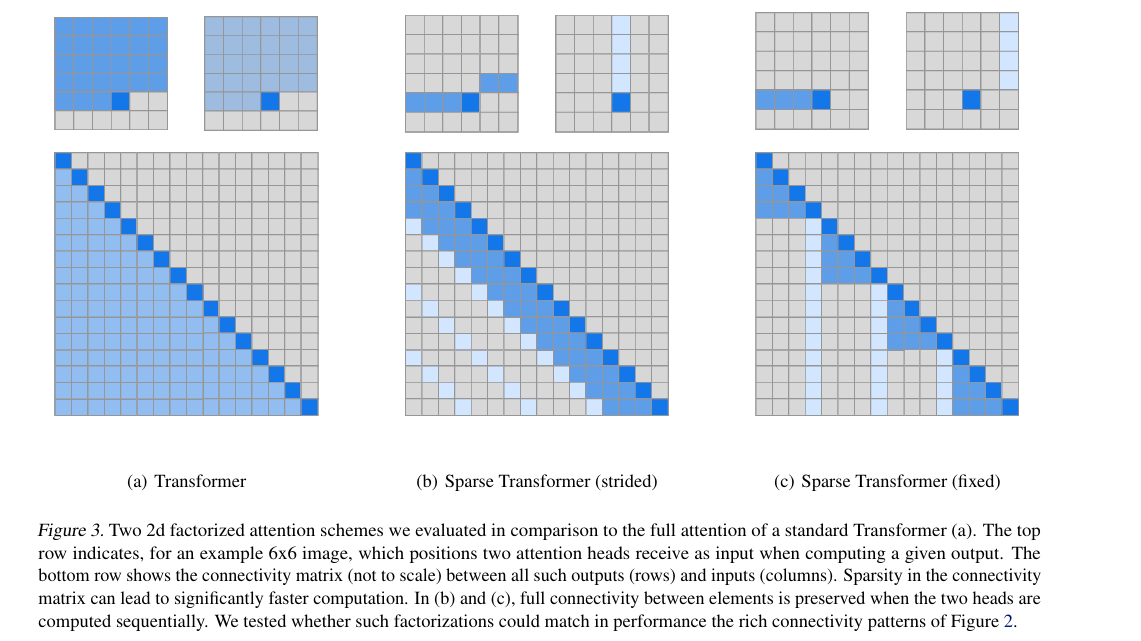
    • One approach is to have one head attend to the previous locations and the other attend to every -th location, where and is called the stride. This gives us strided attention.

      Thus for for and .

      • Limitation: Does not work for data without a periodic structure.

    • Another approach is to use a fixed attention pattern where cells summarize previous locations.

      For , and , where and is a hyperparameter.

      Ideally we want multiple heads attend to distinct sub-blocks of length within blocks of size rather than all heads attending to the same sub-block.

  • In order to incorporate the attention pattern to the transformer mechanism, we consider the following

    • The standard approach using dense attention. Let be the full connectivity pattern where denotes the indices of input vectors to which the -th output vector attends. Define the attention pattern as follows:
    • We can use one attention type per residual block. Let be the number of factorized attention head and the index of the current residual block.
    • Have a single head attend to the locations of pixels that all factorized heads would attend to. This is a merged head. It is more intensive than the previous by .
    • Use multi-headed attention with attention products computed in parallel and concatenated along the feature dimension.
      Where is any choice of attention pattern defined previously. The dimensions of any matrices are reduced by such that the number of parameters is invariant to the number of heads.
      • Typically better for shorter sequences. For longer sequences, the bottleneck is attention so parallelism does not yield benefits.

  • Use learned positional embeddings rather than fixed ones.

  • For long sequences with high memory usage, we use gradient checkpointing. This means, recomputing attention and feedforward blocks during the backward pass.

Sparse Transformers Attention Pattern . Image taken from Child, Gray, Radford and Sutskever (2019)

Sparse Transformer. Image taken from Child, Gray, Radford and Sutskever (2019)

Links §

• Transformer Model
• Attention Mechanism

Footnotes §

1. Child, Gray, Radford, Sutskever (2019) Generating Long Sequences with Sparse Transformers ↩