Heterogeneous MARL

• In the heterogeneous setting, we no longer assume that agents necessarily have the same observation space, action space, or reward functions.

• The core issues with Heterogeneous MARL is that the usual approaches are typically for Homogeneous MARL which does not necessarily extend well to the Heterogeneous setting.

• One approach is to allow for heterogeneity among agent policies. That is, and are different functions when .

  • Caveat: For joint rewards, we have the problem of Credit Assignment — that is, how to determine an agent’s contribution to a state.
  • Caveat: The Miscoordination Problem Even with proper credit assignment, policy updates for agent may interfere with updates for agent resulting in a poor joint policy over all.

• According to ¹, there are two classes of heterogeneous systems (which are not necessarily mutually exclusive).

  • Physical heterogeneity comes from differences in the agents in terms of hardware (sensors and actuators) or physical constraint. This implies different observation and action spaces.
    • Physical heterogeneity can be addressed through homogeneous solutions but with added constraints on the agents.
  • Behavioral heterogeneity comes from components having distinct policy outputs when observing the same input.
    • Same Objective Heterogeneity means that the agents have the same objective function but optimized through heterogeneous behavior.
    • Different Objective Heterogeneity means that the agents have different objective functions that they optimize.

• The inherent trade off between homogeneity and heterogeneity is that of sample efficiency (homogeneous) and resilience / performance (heterogeneous).

HARL §

• ² introduces Comparative Advantage Maximization (CAM) to enhance specialization within multi-agent systems.

  • The general idea is to first Develop a general policy via CTDE. and then guide agents to leverage their comparative advantage.

  • On top of the usual Policy Gradient-based approach, we modify the loss function to include the Mutual Information written as follows for two agents .

  • Agents are identified using IDs (denoted ). Implicitly, all localized inputs depend on .

  • In the first stage, The base policy is trained on states and agent IDs with the goal of maximizing mutual information across agent pairs. Mutual information means agent behaviors are interlinked and aligned while still allowing some room for diversity. In particular, the goal is to maximize the following

  • In the second stage, we use the baseline policy from the first stage. Each agent maximizes its comparative advantage, in such a way that agents learn to specialize. The goal is to maximize the -value of individual actions.

    To ensure evolution, policies are added to the opponent pool for refinement and competition.

    Our objective function is to maximize the following. We denote the base model as . For each , denotes the state of the world where and agent does nothing.

• ³ proposes Heterogeneous MARL (HARL) algorithms for the cooperative setting designed to coordinate agent updates. In particular, the key idea of their scheme is to perform sequential updates on each individual agent’s policy rather than update the whole joint policy,

  • (³ 4) Multi-Agent Advantage Decomposition. In any cooperative Markov games given a joint policy , for any state and agent subset , the following holds for the Multi-agent Advantage.

    That is, a joint policy can be improved sequentially.

  • (³ 6) Let be a joint policy. For any joint policy we have

    Where

    We define as follows. Let be the joint policy, be some other joint policy of agents and be some other policy of . Then

    The sequential update scheme is given below

  

  Sequential HARL. Image taken from ZhonG et al. (2023)
  • In performing the sequential update, we take into account the previous agent updates.
  • (³ 7) The Multi-Agent Policy Iteration with Monotonic Improvement Guarantee monotonically improves. In fact, (Zhong 8) The policy converges to the Nash Equilibrium.

    • The algorithm is not practical however since it (1) assumes the use of the full state space and action space and (2) requires the computation of the KL Divergence.

  • The Sequential HARL algorithm can be made more practical using TRPO and PPO versions as shown below
  HATRPO. Image taken from Zhong et al. (2023)

  

  HAPPO. Image taken from Zhong et al. (2023)

Parameter Sharing Methods §

UAS §

• ⁴ introduces the use of a Unified Action Space (UAS) which consists of semantic representations of agent actions from a latent space of all possible agent actions, particularly in the case when agents are physically heterogeneous (i.e., different constraints or capabilities).

• Action masks are used to generate the agent policies.

• (Yu 1) There exists a fully-cooperative physically heterogeneous MARL problem such that the joint reward with parameter sharing is suboptimal.

  More formally if is the optimal joint reward, and is the optimal joint reward under parameter sharing. Also let denote the probability of action . and there are agents, we have

• Semantic representations come from dividing the action space based on semantics (i.e., what the actions do).

  For all , divide the local available action set sets with different action semantics. The Unified Action Space is defined as

  Clearly .

  To identify different action semantics, we use an Action Mask operator. That is, given an action mask we extract the actions as

• By performing action masking, we are able to use global parameter sharing while maintaining action semantics. We operate on the Unified Action Space with parameter sharing and to extract action semantics, we perform action masking.

• In addition to UAS, we introduce the Cross Group Inverse Loss to facilitate learning and predicting the policy of other agents.

  It is calculated as follows. Let be the action mask for other physically heterogeneous agents. Then the CGI loss is the mean squared error between and . If each agent has an associated independent network branch parameterized by , we have

  Where is the hidden state of an associated GRU which encodes the trajectory. The average is calculated over samples from the replay buffer

  Similarly for value-based algorithms

• The overall pipeline is shown below

UAS pipeline. Image taken from Yu et al. (2024)

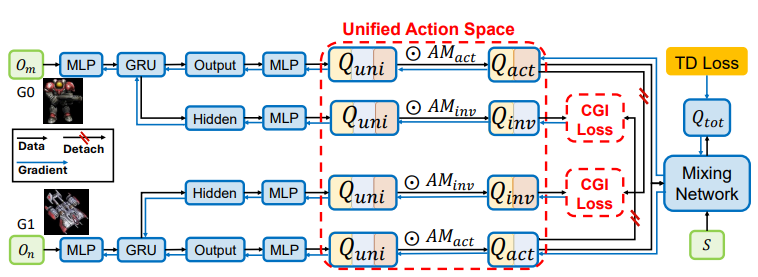
• A version of MAPPO using Unified Action Spaces is shown below. The relevant equations for calculations are as follows

  Each is a hyperparameter that acts as weighting coefficients

U-MAPPO. Image Taken from Yu et al. (2024)

• We can also extend QMIX similarly. The relevant equations are as follows

U-QMIX. Image taken from Yu et al. (2024)

SHPPO §

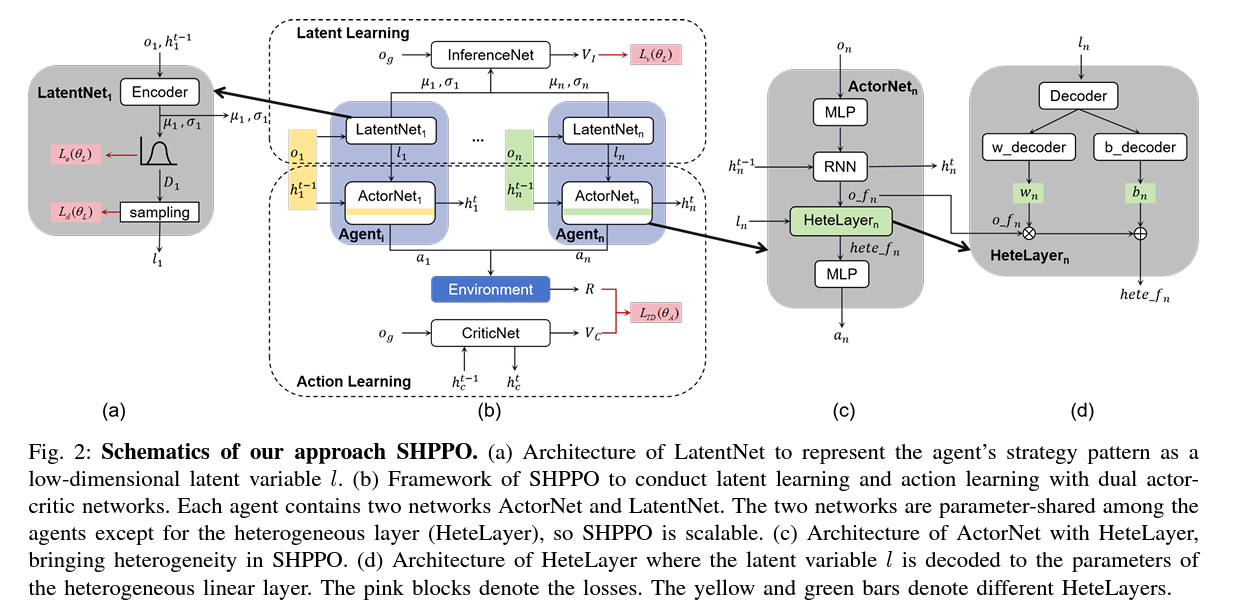
• ⁵ proposes a parameter-sharing based approach but with heterogeneous layers for each agent’s policy network, which are given by a latent distribution learned via an encoder network.

• The strategy pattern of each agent is represented by a latent variable obtained using the encoder network as follows

• To learn the parameters for the encoder, we also include an InferenceNet as a critic that learns to minimize the difference between the value function and the reward. It outputs the value

  • More formally, let be the concatenation of all and ; denotes the parameters of the InferenceNet; are regularization constants; is the entropy function of the distribution; is the latent distribution (in this case, a Gaussian parameterized on ); pertains to normalization.
    • Minimizing means learned latent variables help choose better heterogeneous layers (since we maximize value)
    • Maximizing means latent distributions are more identifiable.
    • Minimizing means latent distributions are more diverse .

• Each is then used to generate a heterogeneous layer. That is, we get the heterogeneous parameters from .

• Limitation: The heterogeneous layers chosen are simple. It is also reliant on the population distribution.

SHPPO. Image taken from Guo et al., 2024

Footnotes §

1. Bettini, Shankar, and Prorok (2023) Heterogeneous Multi-Robot Reinforcement Learning ↩

2. Juang et al. (2024) Breaking the mold: The challenge of large scale MARL specialization ↩

3. Zhong et al. (2023) Heterogeneous-Agent Reinforcement Learning ↩ ↩² ↩³ ↩⁴

4. Yu et al. (2024) Improving Global Parameter-sharing in Physically Heterogeneous Multi-agent Reinforcement Learning with Unified Action Space ↩

5. Guo et al., 2024 Heterogeneous Multi-Agent Reinforcement Learning for Zero-Shot Scalable Collaboration ↩