- Rationale: Regular PGM- based approaches are difficult because (1) it can be difficult to learn a centralized value function that scales with exponential action space; and (2) centralized value functions do not imply efficient decentralized execution. [^valdec_1]
-
The goal is to decompose the following where
is the common reward. -
A simpler utility function can be used for each agent, conditioned only on individual observation history and actions. We denote this with
-
The Individual-Global-Max (IGM) property states that greedy joint actions with respect to the centralized action-value function should be equal to the joint action composed of the greedy individual actions of all agents that maximize their individual utilities.
-
More formally, define both forms of greedy actions as follows
-
The IGM property is satisfied if the following holds for all histories
-
Because of IGM, we can have all agents follow a policy based on their local utility (which is more efficient to compute) and it would be equivalent to the original Centralized Value Function-based policy
-
It also helps establish reward credit since the reward is “common” to all agents.
-
The IGM property is not necessarily satisfied for all environments
-
Linear Value Decomposition
-
Assume a linear decomposition of common rewards. That is
-
The decomposition is as follows. It is guaranteed to satisfy the IGM property
-
Value Decomposition Networks (VDN) maintain a replay buffer containing the experience of all agents and jointly optimizes the loss function

Monotonic Value Decomposition
-
Extends Linear Value Decomposition to apply to cases when the contribution of each agent to the common reward is non-linear.
-
QMIX extends VDN by ensuring that the centralized action-value function is strictly monotonic with respect to individual utilities. That is
- In other words the utility of any agent for its action must increase the decomposed centralized action value function.
-
QMIX uses a mixing network which is simply a standard feedforward Neural Network
- To ensure monotonicity, we assume the mixing network only allows for positive weights.
- The loss function optimized is

QTRAN
-
Monotonic Value Decomposition only provides a sufficient condition but not a necessary condition.
-
The following decomposition gives both sufficient and necessary (under affine transformations) conditions.
Where
-
-
QTRAN trains a network that optimizes the following:
- For each agent, their individual utility functions
- A single network for the global utility function
- A single network for the centralized action-value function
- For each agent, their individual utility functions
-
For the centralized action-value function the following loss function (a TD-error) is minimized
-
For the utility functions, we minimize additional regularization terms given by the following (for the first case in the condition specified above where
-
For the second case, we apply the following
- QTRAN gas a few limitations
- It does not scale well due to relying on joint action space
- It does not directly enforce the necessary and sufficient conditions for IGM, instead using regularization terms. Hence, IGM is not guaranteed.
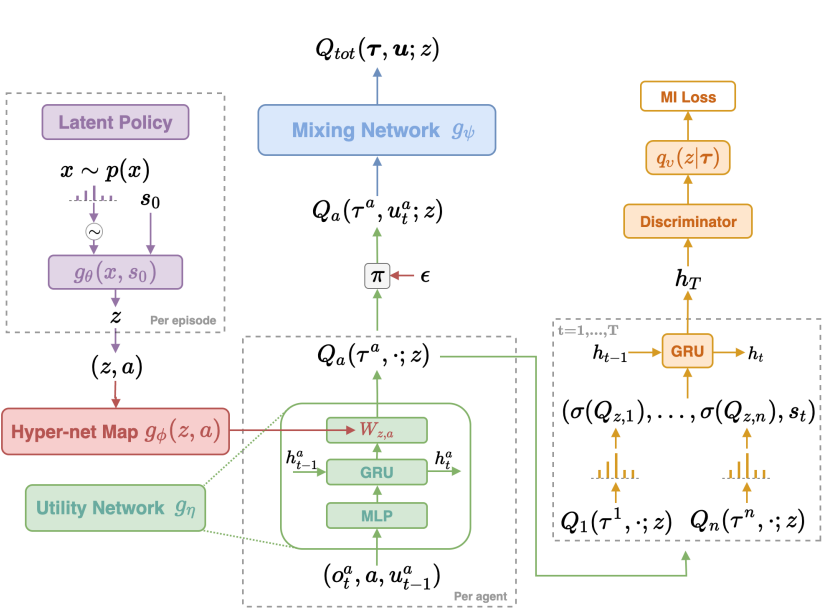
MaVEN
-
1 suggest that representational constraints on the joint action values lead to poor exploration and suboptimality. This is because none of these methods are able to perform committed exploration wherein a specific set of actions (probabilistically unlikely to be chosen in that exact sequence )are required to perform further exploration
-
The monotonicity constraint can prevent the Q-network from correctly remembering the true value of the optimal action (currently perceived as suboptimal
-
Multi-Agent Variational Exploration learns an ensemble of monotonic approximations of QMIX via latent space representation
-
Each model can be seen as a mode of committed joint exploration.
-
A shared latent variable
-
The loss function becomes as follows
-
A hierarchical policy objective is obtained through parameter freezing
-
Another objective makes use of mutual information to encourage diverse but identifiable behavior among policies derived from
A tractable lower bound is provided using a variational distribution
-
-
The complete objective is the following

Links
- Albrecht, Christianos, and Schafer - Ch. 9
- 9.5.2 - derivation of Linear Value Decomposition as well as a proof of it satisfying the IGM property.
Footnotes
-
Mahajan, Rashid, Samvelyan, Whiteson (2020) MAVEN: Multi-Agent Variational Exploration ↩