Families of Graphs

• Empty Graph - the graph with no vertices.

• Null Graph - - the graph with no edges.

• Complete Graph - - the graph where each pair of distinct vertices is adjacent.

• Hypercube Graph - - the graph whose vertices correspond to the vertices and edges correspond to that of a -dimensional hypercube

  • It can also be interpreted as the graph on binary numbers where edges connect tuples which differ in one bit.
  • (Godsil 3.1.1) is vertex transitive.

• Trails, Walks, Paths and Cycles

  • A path of vertices is denoted .
  • A cycle of vertices is denoted

• Eulerian Graph

• Hamiltonian Graph

• Bipartite Graph

• Tree

• Infinite Graph

• Directed Graph

• A circulant graph is defined as follows. Let (see here). Construct a directed graph such that

  If we assume that , then is closed under additive inverses and the graph is undirected.

  That is, a circulant graph is a graph acted on by a cyclic group acting on the vertices of the graph.

• Generalized Johnson Graph

• Line Graph

• Asymmetric Graph

• Vertex Transitive Graph

• Edge Transitive Graph

• Arc Transitive Graph

• s-Arc Transitive Graph

• Distance Transitive Graph

• Cayley Digraph

• Regular Graph

• Moore Graph

• The Halin Graph is a graph constructed as follows. Start with a tree with no vertex of degree and with at least one vertex of degree greater than . Draw on the plane and then connect all leaves to form a cycle.

• The Latin squares of order form a graph as follows. Each entry is represented as a tuple and edges are constructed between triples which agree on one coordinate.

  • It is distance regular but not necessarily distance transitive.
  • It has diameter .
  • It is regular with degree

• The Coxeter Graph

  • It has vertices
  • It is cubic
  • It has girth .
  • Its full automorphism group has size .
  • It acts -regularly.
  • It can be made as an induced subgraph of . In particular, using the orbits of the triples .
  • It can be constructed using the circulants on . Start with the circulants. Then, add more vertices that are adjacent to the corresponding vertices in each circulant.

Coxeter Graph By Watchduck - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=121361030

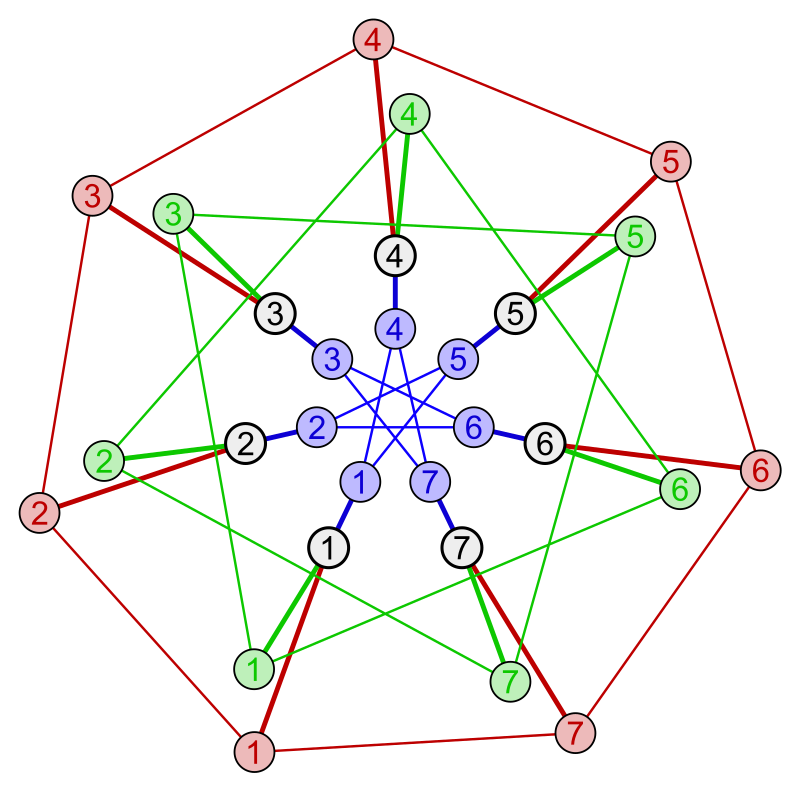
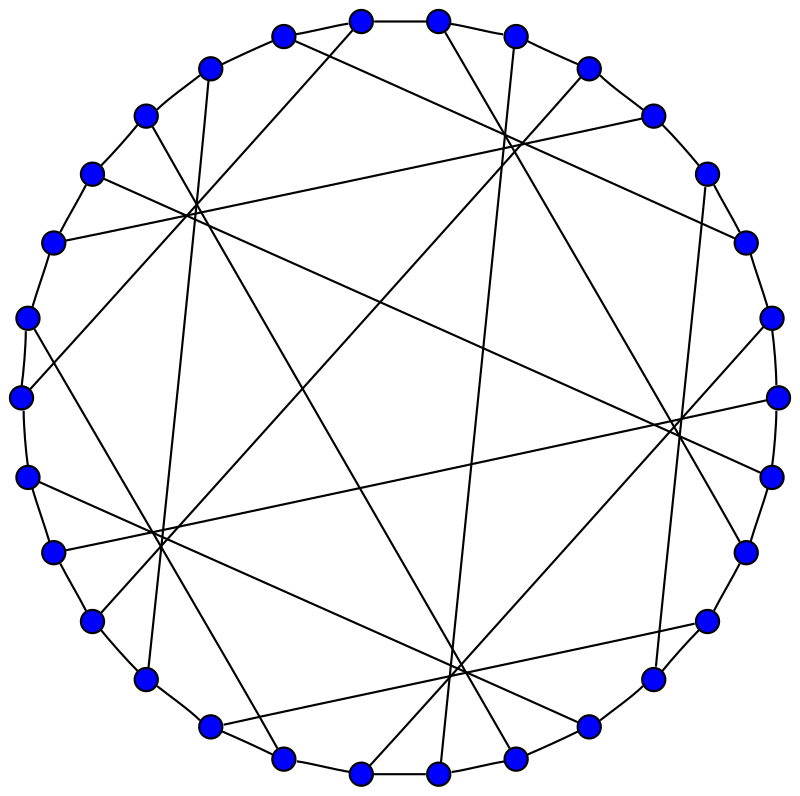
• Tutte’s 8-cage

  • It consists of vertices.

  • There are two equivalent constructions for it:

    • Take the cube and the additional vertex . In each set of four parallel edges, join the midpoint of each pair of opposite edges by an edge. Then join the midpoint of the two new edges by an edge. Then join the midpoint of this edge to .
    • Take the complete graph . Construct a bipartite graph with the edges of as one partition and the -factors as the other. Each edge is adjacent to the three -factors that contain it.

  • It is cubic

  • It is distance regular.

Tutte's 8 Cage Public Domain, https://commons.wikimedia.org/w/index.php?curid=618430

• Levi Graphs - for incidence structure

Links §

• Fundamental Constructs of Graph Theory

• Algebraic Graph Theory by Godsil and Royle

• Introduction To Graph Theory by Wilson