Generalized Johnson Graph

• A Generalized Johnson Graph denoted is defined as follows for . Let be a set of size . Then

  • The Johnson Graph is defined as

  • The Kneser Graph is the graph

  • The Odd Graph is the Kneser graph

    • Each edge in an odd graph has an “odd one out”.

• The Johnson graph is a regular graph with degree

  • In fact, it’s edge transitive.

• For any vertex in say the stabilizer follows

  Clearly, any permutation which permutes the elements in and the elements not in is an element of .

• (Godsil 1.6.1) if , then

  • Proof: Let map from sets to their complements. This map is an isomorphism.

    Every -set has a unique complement, which is an -set.

    Also, if are -sets where then

    The converse is also true: If are -sets, then the intersection of their complements has magnitude .

• (Godsil 1.6.2) If , then the automorphism contains a subgroup isomorphic to .

  • Idea: A permutation on sets does not change the size of their intersections. That is

• (Godsil 4.1.1) is at least arc-transitive.

  • Proof: Any two vertices in that meet at a vertex can be mapped to each other via .

• (Godsil 4.1.2) is at least -transitive.

  • Proof: Consider two -arcs and . By definition, we know that WLOG, we may represent each vertex as
    Thus acts transitively on the -arcs.

• (Godsil 4.5.1) is distance transitive.

  • Proof: We show that . Thus, the automorphism on acts distance transitively.

    First suppose . Note that if , then by definition. Argue by induction and suppose . WLOG, and

    Now, consider adjacent to . so they only differ by exactly one element. In fact, and differ by an element in as if they differed in we would get . WLOG, replace with and clearly as was to be shown.

    Conversely, suppose . Clearly if then is adjacent to . Again, argue by induction but this time on so that . Take such that Therefore, using transitivity, we can ensure that . In fact

    Therefore is adjacent to . They must differ by exactly one element. By extension . Also, clearly since we can construct the path where we iteratively replace the last elements. Both inequalities give us the desired result.

• (Godsil 4.5.2) The odd graph is distance transitive.

  • Proof: Observe that any path in corresponds to the addition of vertex and the removal of another vertex. Clearly, any automorphism which preserves what vertex gets added and removed works and preserves paths. Hence, they preserve distance and so is distance transitive.

Petersen Graph §

• The Petersen Graph is defined as a special Kneser graph

The Petersen Graph By Leshabirukov - Own work by uploader based on http://en.wikipedia.org/wiki/File:Heawood_Graph.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=5788203

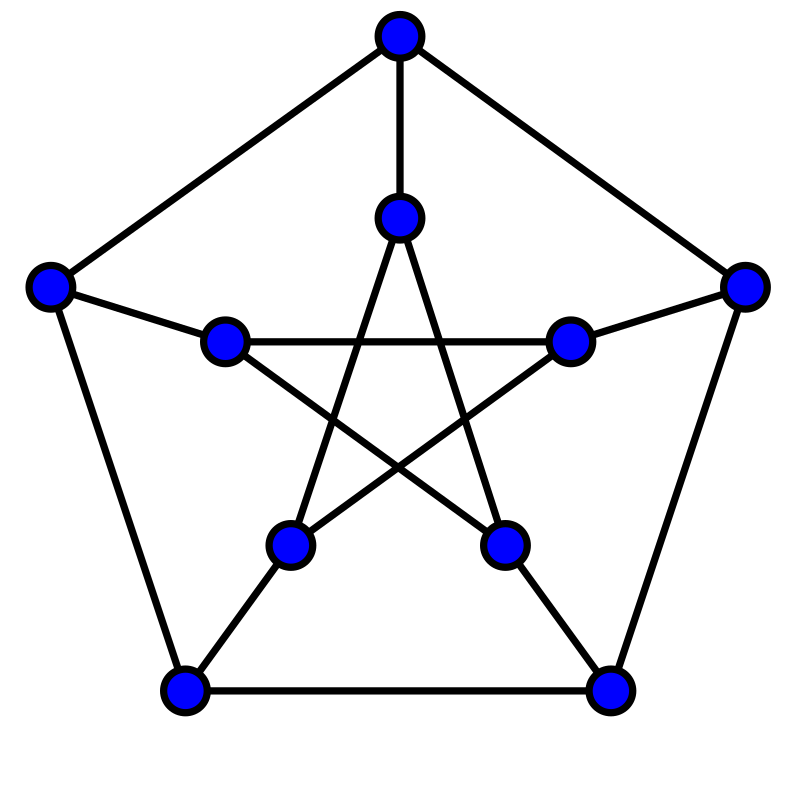
• (Godsil e3.2) The Petersen graph is not a Cayley graph. In fact, it is the smallest vertex-transitive graph that is not a Cayley graph.
  • Proof: Suppose is a Cayley graph on elements isomorphic to the Petersen graph. Since must be order , Either or . In both cases, there are no -cycles, which the Petersen graph contains.
• (Godsil 4.4.1) The Petersen graph cannot be -edge colored.
• The Petersen graph is distance transitive.

Links §

• Algebraic Graph Theory by Godsil and Royle