Bipartite Graph

• Bipartite Graph - it is possible to split the vertex set into two disjoint sets called the bipartition such that each edge is of the form

  • is bipartite if it can be expressed as the union of disjoint, possibly empty independent sets
  • is -colorable.
  • (Wilson 5.1) is bipartite if and only if every cycle has even length.
  • A bipartite graph is semi-regular if it has a proper -coloring such that all vertices with the same color have the same degree.

• Complete Bipartite Graph - given the bipartition of the bipartite graph. , all vertices from are adjacent to all vertices in .

  Here

  • A star graph is a special case, .

• Generalized polygon - special classes of bipartite graphs.

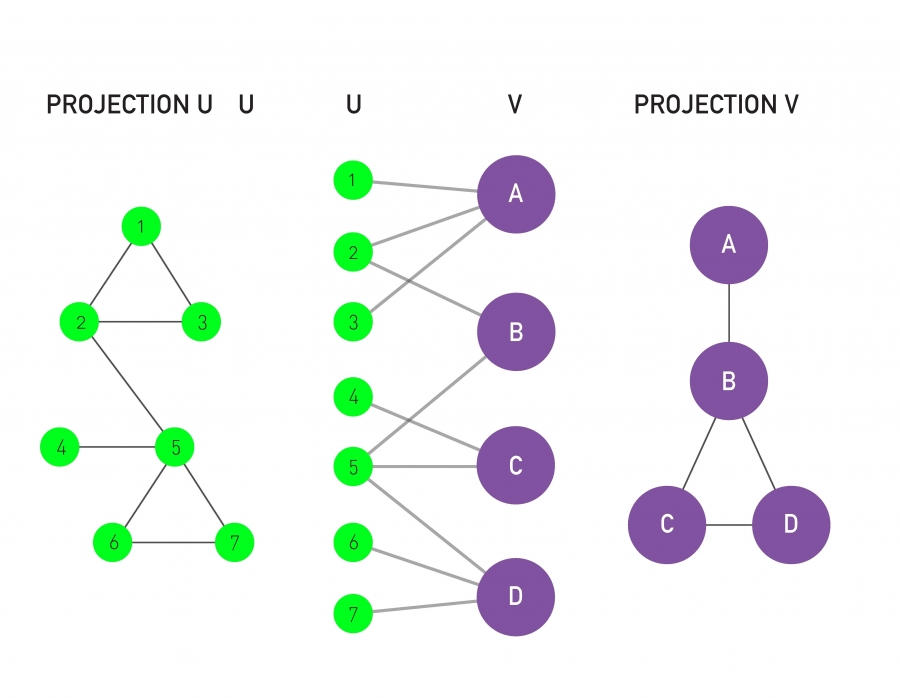
• A Bipartite Network Projection is an operation for simplifying a bipartite graph.

  Let be bipartitions of the bipartite graph. Then, its projection on * is defined as a graph whose nodes are the same as the vertices of , and two nodes are connected if and only if they are linked to the same node in .

  A similar projection on can also be defined.

  

Links §

• Introduction To Graph Theory by Wilson