Group Isomorphism

• Let and be binary algebraic structures. A bijection is an isomorphism if

  We say (i.e., the groups are isomorphic.

  • It is a bijective Group Homomorphism

• A structural property is a property that is preserved under isomorphism.

• (Fraleigh 8.15) Let and be groups and be a one-to-one function such that . Then the image is a Subgroup of and provides an isomorphism of with . In other words

• As a corollary to (Fraleigh 13.18) a mapping can be shown to be an Isomorphism by showing the following

  • is a homomorphism
  • is onto.

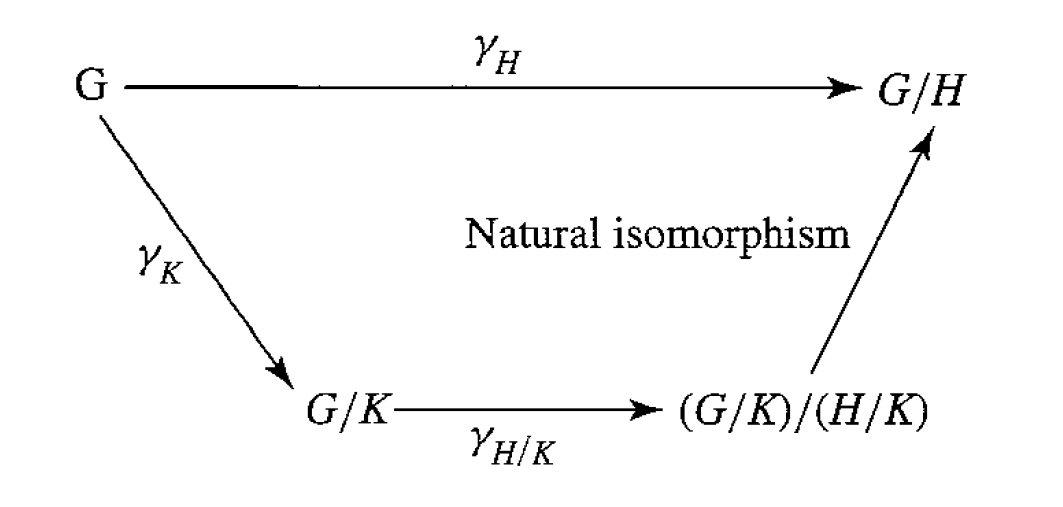
• (Fraleigh 34.5) Second Isomorphism Theorem Let and . Then

  (see Normal Group)

  • Idea: Let be the canonical homomorphism for such that We have the following commutative diagram:
    

Diagrammatic Proof Sketch of the Second Isomorphism Theorem. Original Image

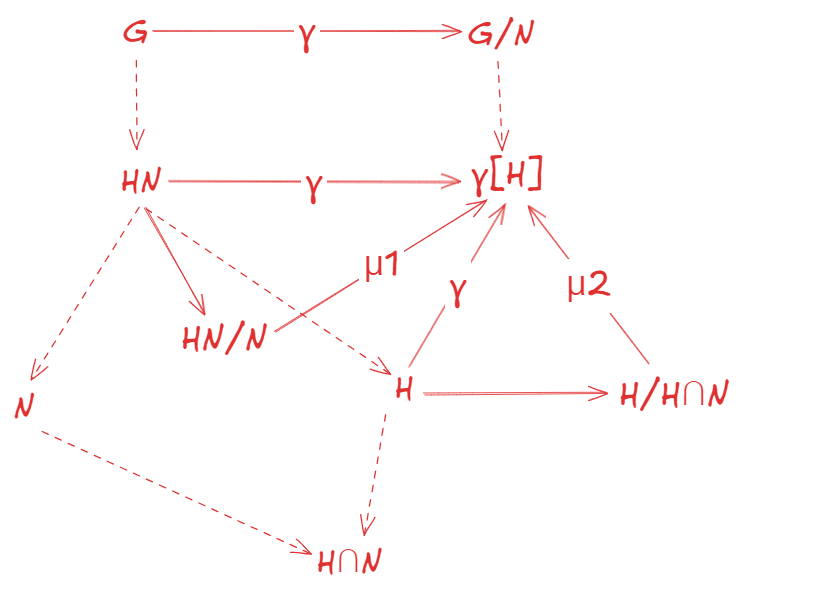
• (Fraleigh e34.9) Let with and . Then

• (Fraleigh 34.7) Third Isomorphism Theorem. Let with . Then

  (see Factor Group)

  • Idea:

Diagrammatic Proof Sketch of the Third Isomorphism Theorem. Image taken from Fraleigh

Topics §

• Group Isomorphism

Links §

• A First Course in Abstract Algebra 7th Edition by Fraleigh
• Fundamental Constructs of Group Theory