is normal if its left and right cosets coincide i.e.
-
A group is a simple group if it is nontrivial and has no proper nontrivial normal subgroups.
- That is, it does not have a factor group that is not the trivial subgroup or the group itself.
-
(Fraleigh 14.13) The following are equivalent conditions for
to be normal. and , the following holds is invariant under all inner automorphisms of . That is
-
(Fraleigh e14.31) Let
, then the intersection is also normal -
(Fraleigh e14.34) If
has exactly one subgroup of a given order, then is a normal subgroup of . -
A maximal normal subgroup of a group
is a normal subgroup such that there is no proper normal subgroup -
(Fraleigh 15.18)
is the maximal normal Subgroup of if and only if is simple. -
(Fraleigh 34.4) If
and , then Also if
is also normal in , then is also normal in . - Idea: To show the theorem, show that
is a subgroup of . Since is the smallest subgroup containing , clearly if is a subgroup .
- Idea: To show the theorem, show that
-
Let
and . Then -
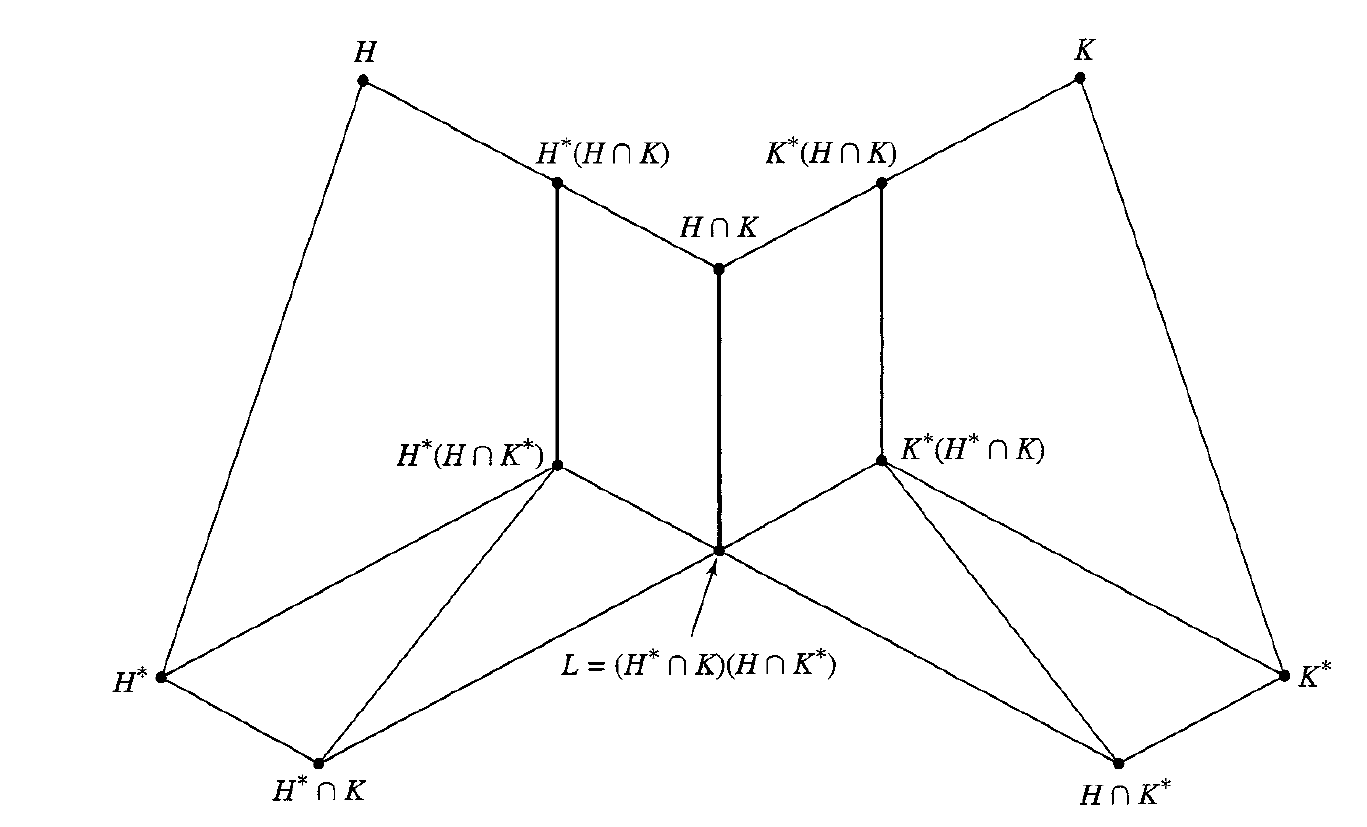
(Fraleigh 35.10) Zassenhaus Lemma / Butterfly Lemma. Let
and and . Then -
-
-
-
-
Proof: Let
and be defined as the theorem. Clearly all products involved are groups by (Fraleigh 34.4). To show the normal subgroup relation, we must show that and similarly . All normal subgroup relations in the theorem then follow immediately from (Fraleigh 34.4). Let
To show the isomorphism, define the homomorphism
such that for and , we have It is easy to show that
is a well-defined homomorphism. It is also onto. Thus Therefore
. The First Isomorphism Theorem guarantees the isomorphism.
-