Graph View

Backlinks

The Library

Search

SearchSearch

Group Homomorphism

Jan 06, 2025, 3 min read

  • Let and be binary algebraic structures. A mapping is a homomorphism if

    • The homomorphism property says that the product of the maps is equal to the map of the products.

  • (Fraleigh e13.49) The composition of homomorphisms is a homomorphism.

  • (Fraleigh 13.12) Let be a homomorphism.

    • The identity is preserved. If is the identity of , then is the identity of

    • The inverse is preserved.

    • Subgroups are preserved.

    • Subgroup inverses are preserved

    • (Fraleigh 15.16) Normal groups are preserved.

  • Let be a homomorphism. The kernel of , denoted is defined as the subgroup

    Where is the identity of .

    • We may think of this as the set of points which the homomorphism maps to a singularity
    • Note that by definition

  • (Fraleigh 13.15) If and , then we have the cosets of as

    It follows that the partition of into cosets is the same.

    • Proof: We have

  • (Fraleigh 13.18) A homomorphism is one to one if and only if .

    • Intuition: Every element can be written as where . Clearly a homomorphism can only be one-to-one if and only if maps to a unique element in , if and only if are unique, if and only if is unique, if and only if and only. That is, and so

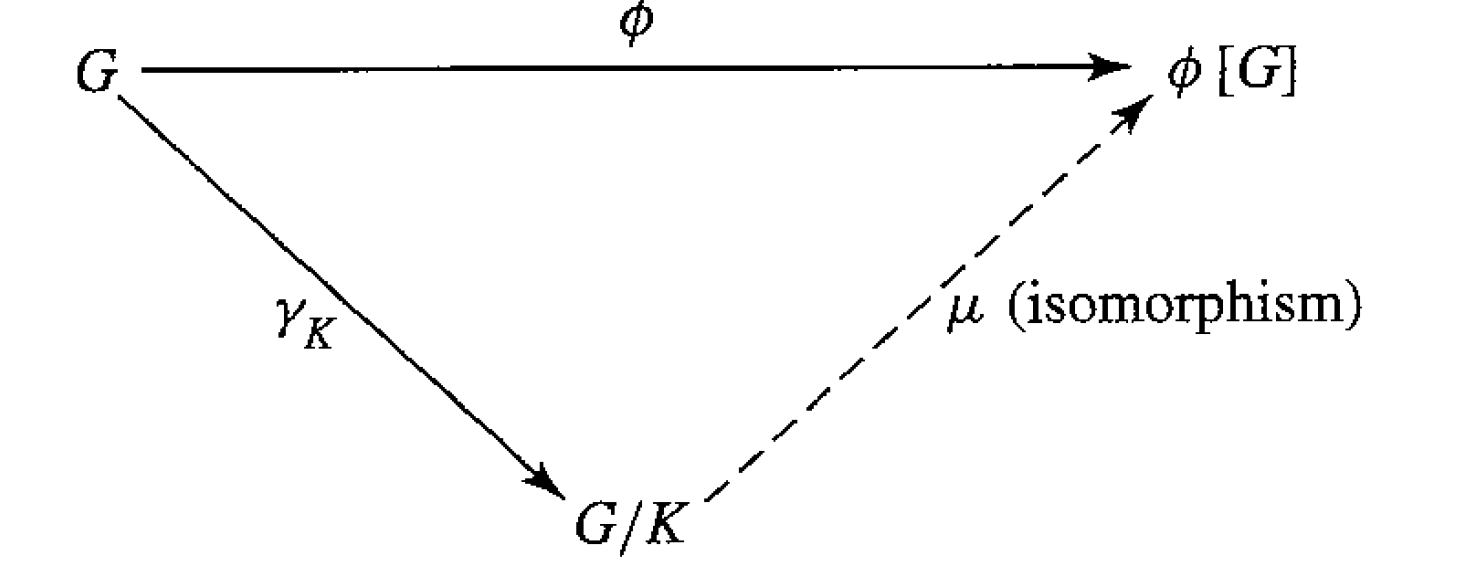
  • (Fraleigh 14.11, Fraleigh 34.2) The Fundamental Homomorphism Theorem / First Isomorphism Theorem. Every Factor Group gives rise to a natural homomorphism.

    Let be a homomorphism with kernel .

    Then is a group and given by is an isomorphism. In other words

    If is the homomorphism given by , then

    We refer to and as the natural (canonical) isomorphism and natural (canonical) homomorphism respectively.

    • If is onto, then the isomorphism changes to
    • (Fraleigh 13.20) is a normal subgroup of
    • (Fraleigh 34.3) Let and be the canonical homomorphism. Then the map from the set of normal subgroups of containing to the set of normal subgroups of given by is bijective.

First Isomorphism Theorem. Image taken from Fraleigh
  • An isomorphism is a homomorphism that is bijective.
  • An endomorphism is a homomorphism from to itself.

Links