Decision Time Planning

Decision Time vs Background Planning §

• We may combine background planning and decision planning (i.e., do decision-time planning then cache the results for background planning).
• Decision-time planning is useful when we do not require fast responses (since at each step we have to do the planning algorithm.)
• Background planning is useful when we require low latency (since executing the plan constitutes a look up.)

Heuristic Search §

• It makes use of the current value function to improve action selection. It is planning as part of a policy computation.
• The approximate value function is applied to leaf nodes and then backed up towards the root of the search space (the value at the current state is the max value of its successors)
• Backup stops at the current state. The model then chooses the best action based on the heuristic.
• Conventionally, the value function doesn’t change, but we can design methods that update the value function.
• It also helps in pruning the search space by growing only on the actions that are likely to yield the best states. It is synergistic too, as it is in these states that we want the value function to be accurate.
  • It also allows us to deal with imperfect action-value functions by looking one step ahead.

Rollout Algorithms §

• Decision-Time planning algorithms based on Monte Carlocontrol (to rollout is to allow the simulation to play out multiple times)
• The goal: Estimate the action values for the current state and based on the rollout policy.
  • They estimate action values for a given policy by averaging the returns of many simulated trajectories that start with each possible action and then follow the given policy.
• The policy improvement theorem applies to Rollout Policies as well. The policy that selects an action in that maximizes the estimates of and thereafter follows improves over .
  • The performance of the improved policy depends on properties of the rollout policy and the ranking of actions produced by the Monte Carlo value estimates.
  • An important tradeoff: Better rollout policies = more time needed to simulate trajectories.

Monte Carlo Tree Search §

• A rollout algorithm but where we allow accumulating value estimates to direct simulations towards more highly-rewarding trajectories.

• Applied in: AlphaGo.

• The core idea of MCTS is to successively focus multiple simulations starting at the current state by extending the initial portions of trajectories that have received high evaluations from earlier simulations

• It may or may not retain action-value approximations, although in many implementations, it retains the selected actions in the previous step.

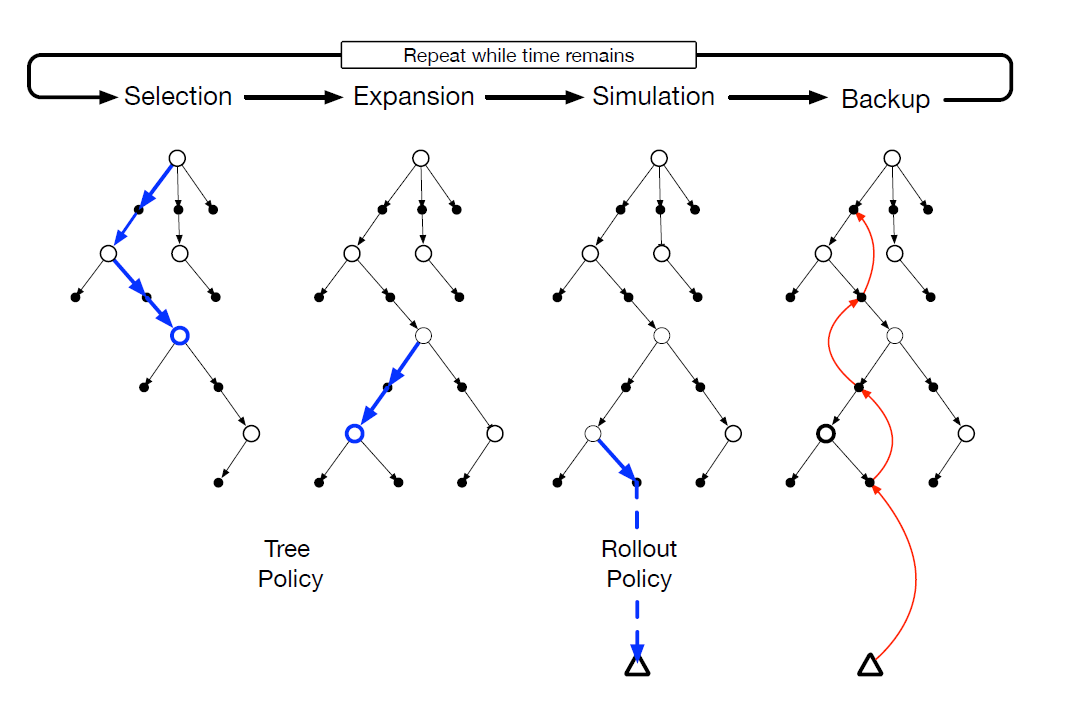
• The key steps:

  • Selection - starting at the root node, a tree policy based on the action values attached to the edges of the tree traverses the tree to select a tree node.
  • Expansion - expand the tree from the selected leaf node by adding successors based on unexplored actions.
  • Simulation - from the selected node or from one of the newly added child nodes, simulate a complete episode selected by the rollout policy.
    • So that select actions first by the tree policy, and then beyond by the rollout policy.
  • Backup perform updates or initializations on the action values. We do not save values for the states and actions visited beyond the tree.

• It benefits from online, incremental, sample-based value estimation, and policy improvement.

• The approach focuses on trajectories whose initial segments are common to high-return trajectories previously simulated.

• By incrementally expanding the tree, it grows a lookup table to store a partial action-value function. Thus, it does not need to globally approximate the action-value function, while it can also use past experience.

Monte Carlo Tree Search. Image from Sutton and Barto (2017)

Monte Carlo Tree Search. Image taken from Albrecht, Christianos and Schafer

AlphaZero §

• AlphaZero is an approach which combines Monte Carlo Tree Search, Self Playand deep learning.
• At its core it is MCTS. However, it is trained using self-play (either using current versions of the policy or past versions).
  • During a MCTS simulation, the current agent chooses all the actions in each time step (i.e., playing against itself).
  • The agent’s observations (if it is simulating the opponent’s turn) is made to be ego-centric.
• In addition, it learns an evaluation function
  Which learns the expected outcome from state as well as a vector of action-selection probabilities given current state . is used to guide action selection during simulation.
• The model is trained to minimize the following loss function (with L2 regularization).

Links §

• Sutton and Barto Ch. 8.8 - 8.11

• Albrecht, Christianos, and Schafer - Ch. 9.8

• A Unified View on Planning and Learning - more on planning and learning algorithms.

• Alpha Zero and Monte Carlo Tree Search

• Monte Carlo Tree Search Tutorial