Network Communities

• A community is a group of nodes within a network that have a higher likelihood of connecting to each other than to nodes from other communities.

• The Community Hypotheses are fundamental to network communities

  • Fundamental Hypothesis - A network’s community structure is uniquely encoded in its Wiring diagram
  • Connectedness and Density Hypothesis - a community is a locally dense, connected subgraph of the network
  • Random Hypothesis - random networks lack an inherent community structure
  • Maximal modularity Hypothesis - for a given network, the partition with maximum modularity corresponds to the optimal community structure

    • The modularity measures the quality of a community partition in a network.

      More formally, let

      be the number of nodes be the number of links be the number of community, denote the adjacency matrix of the network. denote the expected number of links between nodes and if the network was randomly wired.

      For a community , let

      be the number of nodes be the number of links be the total degree of the community

      The modularity of a community is denoted and defined as

      It is the difference between the partition of the network and the randomly wired network.

      The modularity of the whole network is simply the sum of the modularities of the communities.

    • Higher Modularity implies a better community structure.

    • Zero Modularity implies the community structure is no better than aRandom Network.

    • Negative Modularity implies no community structure between the nodes.

• The internal degree of node in a network is the number of links that connect o other nodes in its community . It is denoted .

• The external degree of node in a network is the number of links that connect to other nodes outside of its community . It is denoted

• A strong community is one where

• A weak community is one where

Community Detection Algorithms §

• Community Detection is a problem in the context of networks. Given some network , we wish to find its community structure — the number of communities and their sizes.

  • The community size distribution which captures the sizes of the communities in the network is, according to empirical studies, an intrinsic property of the network.

• Community detection via a brute-force approach is computationally expensive (to be exact, it scales with the Bell Numbers , so it has exponential time complexity).

  Thus, we want algorithms that can uncover the underlying community structure of a network.

Hierarchical §

Ravasz Algorithm §

• The Ravasz Algorithm is an agglomerative Clustering algorithm for use in community detection

• It consists of the following steps

  • *Define the distance matrix between node pairs. *

    This captures the fact that nodes rom the same community tend to be similar. We do this using the Topological Overlap Matrix (see here)

  • Measure the similarity of communities using unweighted average linkage clustering

  • Perform agglomerative clustering. Merge communities with the highest similarity, and then repeat step 2.

    Because clustering is agglomerative, we start with all nodes being their own communities, and we progressively merge communities together.

• The The time complexity of each of the above steps are Which means the time complexity is

Girvan-Newman Algorithm §

• The Girvan-Newman Algorithm is a divisive clustering algorithm.

• It consists of the following steps

  • Define the distance matrix between node pairs. The distance between node pairs is determined by centrality. For computational performance, we use link betweenness centrality.

    *Higher centrality means nodes are more likely to belong to different communities. *

  • Initialize by having all nodes in one community.

    Remove the link with the largest centrality. In case of a tie, choose one link randomly.

    Then, recalculate the centralities of all links for all clusters. Repeat until all links are deleted.

• The time complexity of the algorithm is determined by the calculation of the centrality.

  Using link betweenness, this centrality is (where and are the number of links and nodes respectively).

Limitations §

• It assumes a hierarchy exists in the network.
• By the density hypothesis, networks can be partitioned into communities that are weakly connected to other communities. However, this goes against the fact that real networks are scale free
• It only gives a family of community structures rather than one that is correct, contradicting the fundamental hypothesis.
• These issues are resolved using the Hierarchical Network Model

Modularity-Based §

Greedy Modularity Maximization Algorithm §

• The following greedy algorithm aims to maximize the modularity of a given network

• It works as follows

  • Assign each node to its own community

  • Inspect each community pair connected by at least one link, and compute the modularity difference (denoted ) obtained if we merge them.

    Merge the communities with the largest .

  • Repeat the above until all nodes merge into a single community.
    Record modularity for each timestep

  • Select the partition for which is maximal.

• Each calculation for each can be done in constant time.

  We require computations in step 2.

  Updating the communities after merging requires .

  The complexity is

Louvain Algorithm §

• The Louvain Algorithm is a proposed alternative to the greedy modularity maximization algorithm that aims to have better scalability

• The procedure is as follows:

  • Start with a Weighted network of nodes and assign nodes to different communities

    Evaluate the gain in modularity if we place node in the community of one of its neighbors .

    Move to the community of when the modularity gain is the highest, but only if the gain is positive.

    The gain is calculated as follows

    Let be a community be the sum of the weights inside be the sum of the link weights of all nodes in . is the total weight of the links incident to be the sum of the weights of the links from to nodes in be the total weight of the network.

    Do this for all nodes until no further improvement can be achieved

  • Construct a new network whose nodes are the communities identified in step . The weights of the links between nodes is the sum of the weight of the links between nodes in the corresponding communities. Links between nodes of the same community lead to weighted self loops.

  • Repeat step 1. Iterate until there are no more changes and maximum modularity is attained.

• The computations scale linearly with . In subsequent passes, the number of nodes and links decreases. It is thus at worst

• Storage is the limiting factor of the algorithm.

Limitations §

• There is a resolution limit wherein there is a threshold where modularity-based approaches fail to capture communities smaller than this threshold. This is because *modularity maximization forces smaller communities into larger communities

• The change in modularity brought by merging two communities and is given by

  Where denotes the number of links that connect the nodes in community with community be the total degree of be the total degree of .

  • If and are distinct communities, they should remain distinct when is maximized. However, this is not always the case.

  • f , then if there is at least one link between the two communities, so B$ must be merged.

  • If , then

    And the modularity increases by merging and into a single community, even if they are otherwise distinct.

    This arises when are below the resolution limit.

  • Because real networks contain many small communities, modularity is not well suited for these.

CFinder §

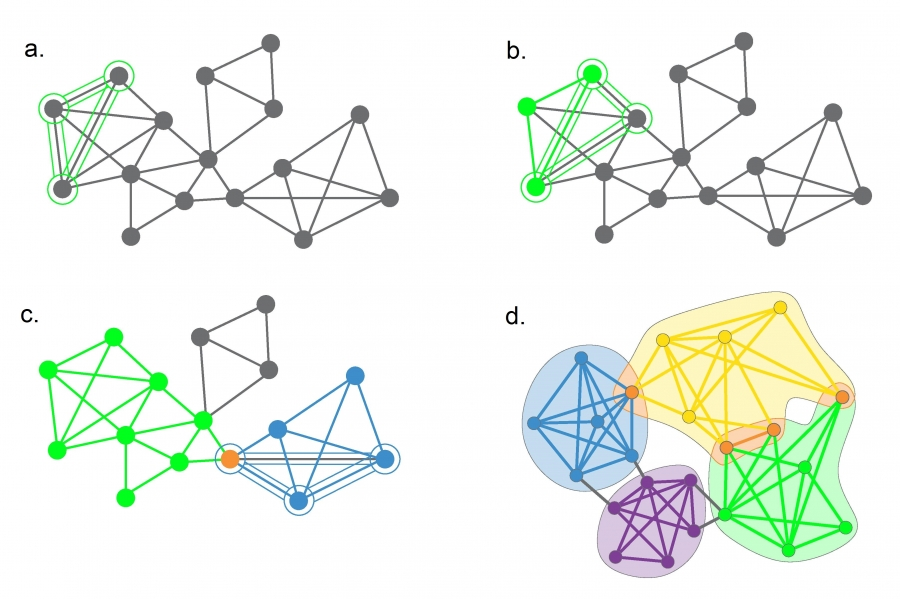
• The Clique Percolation Algorithm interprets communities as the union of overlapping cliques.
• We define the following terms
  • Two -cliques are considered adjacent if they share nodes. (figure )
  • A -clique community is the largest component obtained as the union of all adjacent cliques.(figure )
  • -cliques that cannot be reached from a particular -clique belong to other -clique communities (figure )

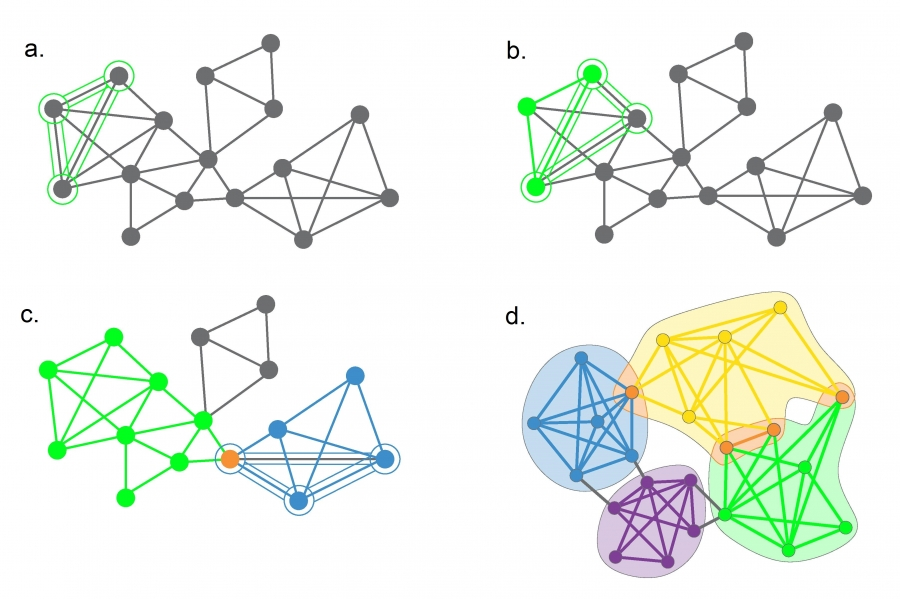
• The algorithm identifies all cliques and builds an overlap matrix whose entries denote the number of nodes shared by cliques and identified by a percolation process of adding nodes to existing communities, provided it has sufficient overlap with the current clique being identified.

• It allows for nodes to belong to more than one community.

• Finding cliques in the network grows exponentially (i.e., ).

• To interpret the overlapping community structure of a network, we must compare it to the community structure obtained for the degree randomized version of the network.

• A large -clique community emerges in a Random Network only if the connection probability exceeds the threshold

  Thus, we expect only a few isolated -cliques. Once , where is the link probability, we expect cliques that form -clique communities.

  • Thus, -clique communities naturally emerge in sufficiently dense networks

Link Clustering §

• The link clustering algorithm by Ahn, Bagrow, and Lehmann captures the fact that while nodes can belong to multiple communities, links tend to be more community specific. The links define the precise relationship between community members.

• It identifies links with a similar topological role in a network and then explores the connectivity patterns of the nodes.

• It is performed as follows.

  • Identify the link similarity between links to obtain a link similarity matrix.
  • Apply hierarchical clustering on the matrix using single linkage clustering.

• Performance wise, it is quadratic.

  • The calculation of similarity for nodes and depend on the degrees , and requires steps. For typical networks, this remains as roughly quadratic time .
  • Clustering itself requires steps
  • In total, the algorithm requires . That said, the is technically a loose upper bound, and can be brought down when considering the degree exponent. For scale free networks, it is .

Infomap §

• Infomap is an algorithm that performs community detection, by minimizing the length of the string needed to represent the network topology as viewed from a random walk

• Consider a network partitioned into communities. We wish to encode in the most efficient fashion the trajectory of a random walker on this network. This is based on the observation that the random network will tend to get trapped into communities.

  We do this by the following procedure:

  • Assign one code to each community via Huffman coding. This code is encoded in the index codebook

  • Assign codewords for each node within each community. This codeword can be reused in different communities

    We then optimize by minimizing

    Where is entropy is the probability that the random walker switches communities.

    • The first term of the formula corresponds to the average number of bits to represent the movement between communities.
    • The second term corresponds to the average number of bits to represent the movement within communities. is the entropy of within-community movements.

• The goal is to minimize over all possible partitions. We can use Louvain for this except we minimize instead of modularity.

• The computational performance is on par with the Louvain Algorithm. It is or .

Benchmarks §

• We can compare the predicted communities of the algorithm to those planted in the benchmark as follows.

  • Consider an arbitrary partition into non-overlapping communities. At each step, randomly sample a node and record the label of the community it belongs to. This gives the probability distribution on whether or not a node belongs to .

• Consider two partitions of the same network, one being the benchmark (ground truth), and the other partition predicted by the algorithm. Each partition has its own and distribution. Consider the joint distribution and calculate the normalized mutual information .

  • If is high, then the detected partitions are identical. Which means, the community detection algorithm can correctly identify community structure.

• When the link density within communities is high compared to their surroundings, most algorithms accurately identify the planted communities

• *The accuracy is benchmark dependent. *

Girvan-Newmann Benchmark §

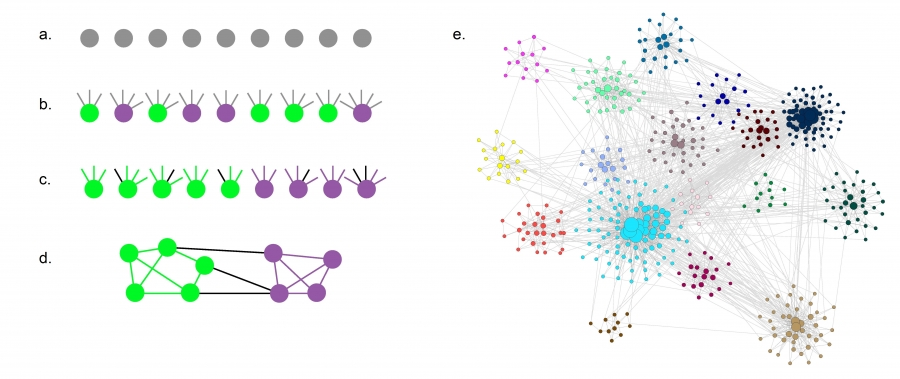
• The Girvan-Newmann benchmark generates a random graph where all nodes have comparable degree and all communities have identical size.

• The usual benchmark consists of nodes partitioned into communities. Each node is connected with probability to the nodes in its communities and to nodes in the other three communities.

• The control parameter captures the density differences within and between communities.

  • For small , the algorithm performs well when nodes are more likely to cluster than connect to other communities.
  • For large , the algorithm drops in performance since the community structure is more blurred as its density becomes comparable to the link density of the rest of the network.

• The main limitation with this benchmark is that it generates fat-tailed networks, which may not be in line with that observed i nreal networks.

Lancichinetti-Fortunato-Radicchi Benchmark §

• The Lancichinetti-Fortunato-Radicchi benchmark generates a random network for which *degree distribution and community size distribution follow power laws. *

• The procedure is as follows

  • Start with nodes. Assign each to a community of size , where
  • Assign each node a degree sampled from a power law distribution where .
  • Each node of a community receives an internal degree and external degree .
  • The stubs of nodes of the same community are randomly attached to each other until no more stubs are free. Thus we maintain the sequence of internal degrees of each node in its communities. The remaining stubs are attached to nodes from other communities.

Evolving Communities §

• The following are empirical findings observed in social networks

• Growth: The probability that a node joins a community grows with the number of links that the node has to members of that community

• Contraction: Nodes with only a few links to members of their community are more likely to leave the community than nodes with multiple links to community members.

  • In weighted networks the probability that a node leaves a community increases with the sum of its link weights to nodes outside the community.

• Death : The probability that a community disintegrates increases with the aggregate link weights to nodes outside the community.

• Age: Older communities tend to be larger.

• Scalability: The membership of large communities changes faster with time than the membership of smaller communities.

Links §

• Barabasi
• Fundamental Constructs of Network Science