Characterizing Real Networks and Network Phenomena

Real Networks §

Degree Distributions §

• In real networks we can observe the following properties in their degree distributions

  • Low Degree Saturation - It can be see as a flattened for . This indicates that we have *fewer small degree nodes than that is expected from a power law.
  • High Degree Cutoff - This manifests as a rapid drop in for . Effectively, this indicates that the largest hub is smaller than predicted in the power law.
    • This emerges if there are inherent limitations in the number of links the nodes can have.

• Deviations from the power law imply that

  Where denotes the saturation cutoff denotes the high degree cutoff.

• Real networks do not have a degree distribution that is Poisson (see Barabasi Ch. 3.5)

  • The probability of observing a node with large degree decreases exponentially given as

  • The bounds of the degree cutoff is given with a probability distribution

Non-Alignment with Random Networks §

• Real Networks are not random. Random networks do not capture certain things in practice.

  • Real Networks are not Poisson
  • The average clustering coefficient of a random network is different to the average clustering coefficient in a network. In real networks, the average clustering coefficient is related to the degree of the node, which is not the case for random networks.
  • The connectedness of a Random Network is different from how it is in practice. The condition in Erdos-Renyi’s Theorem on Connectivity does not hold for real networks.

• Real networks are sparse. That is, they have significantly less links than the theoretical maximum. ¹

• Real networks are supercritical. Real networks have giant components. By Erdos-Renyi’s Theorem on Giant Components, in a real network .
  • Most real networks are not connected, in which case the giant component co-exists with other smaller components.
  • Erdos-Renyi’s Theorem on Connectivity suggests that

Network Robustness §

Network Degree Correlation §

Other Characteristics §

• Real networks have initial attractiveness. This has two implications

  • It increases the degree exponent and makes the network more homogeneous and reduces the size of hubs.
  • It favors the small degree nodes over the larger hubs and weakens the role of Preferential Attachment.
  • It generates low degree saturation.

• Many real networks display hierarcical modulairty which means hierarchies naturally form

• Many real networks have small communities

Network Phenomena §

• Many real networks are scale free which results in some interesting properties

  • The fact that many real networks are scale free means most real systems have “centers of interest” (i.e., hubs). These hubs are a double edged sword, they provide connectivity to the system, while also introducing vulnerabilities such as being superspreaders of pathogens.
  • However, not all real networks are scale-free.. In particular, the networks of material sciences, and the network of power grids do not appear to follow the scale-free property.
  • It appears that, for the scale-free property to emerge, nodes need to have the capacity to link to other nodes. Otherwise, the scale-free property is absent in a system that limits the number of links a node can have (i.e., in a scenario where there are limits to growth)
  • The Matthew Effect is the tendency of individuals to accrue social or economic success in proportion to their initial level of success. The rich get richer and the poor get poorer.

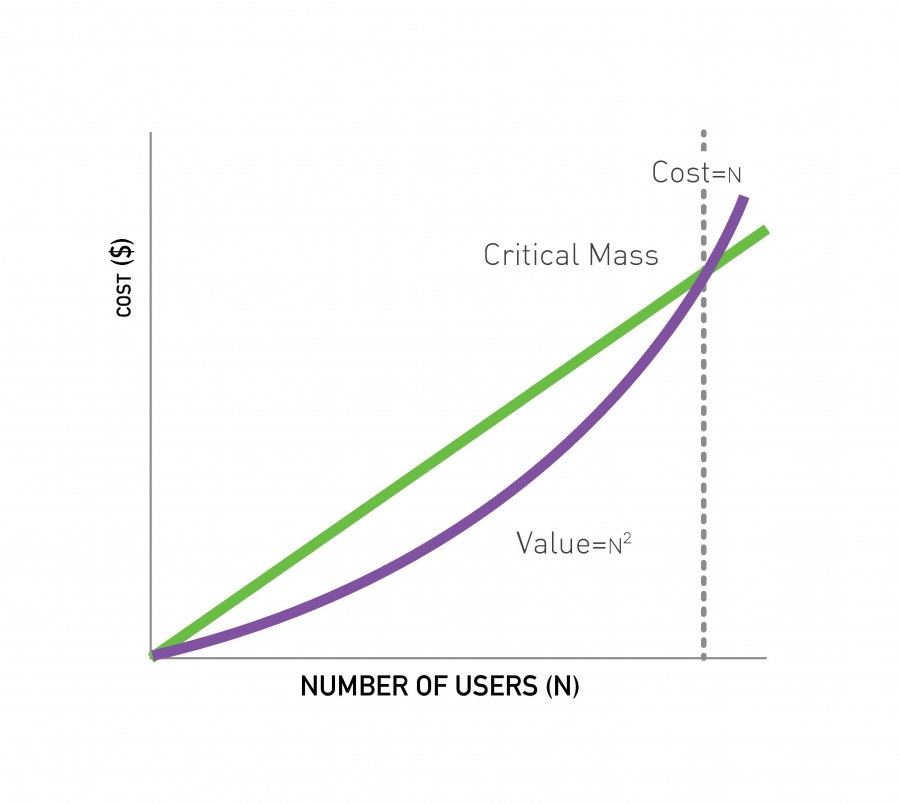
• Metcalfe’s Law states that the value of a network is proportional to the square of the number of nodes in the network.

  • *The more individuals use a network, the more valuable it becomes.
  • The value of a service is proportional to the number of connections it can create. A service becomes profitable as a result if the number of connections surpasses the number of nodes.
  • Some limitations of this law:
    • Most real networks are sparse which means that actually the value only grows linearly rather than quadratically.
    • If the network is weighted, then not all links are of equal value.
    

• The cascading effect of failures is apparent. The size distribution of the failure follows a power law. Most cascades are too small to be noticed. However, a few are huge and have large impacts.

• The Friendship Paradox is a phenomenon, where on average, an individual’s friends have more friends than that individual

  This can be explained as a sampling bias. People who have more friends are more likely to be in one’s own friend group (i.e., because social networks are scale free). In other words, one is less likely to be friends with someone who has very few friends (i.e., preferential attachment).

Links §

• Network Science by Barabasi
• Fundamental Constructs of Network Science

Footnotes §

1. In practice, this means that storing a network can be done using sparse matrices. ↩