-
The Small World Property is a network property that holds when the average distance
grows proportionally to the logarithm of the number of nodes in the network. That is - Intuitively, the above simply says that in a network with the small world property, a typical path will consist of only a few nodes compared to the size of the network.
- Also, the above relation captures the fact that for dense networks where
, the average path length is lower.
Derivation of the Small World Property
- We are motivated by the fact the expected number of nodes up to the distance
from our starting node is obtained by the geometric series Note that, thus the distances have a maximum such that And if, we may simplify the geometric sum above as And we derive the small world property using
- In practice,
above may be reinterpreted as the average distance since for most networks, the actual maximum distance is dominated by a few extremal paths, whereas is averaged over all nodes in the network. Thus, in actuality, the small world property is that
Small World Networks
- A small world network is a network for which the small world property holds and for which average clustering is high.
- It can be described as an interpolation between a regular network and a random network. As such, it can be seen that it has a Poisson degree distribution since high degree nodes remain absent from it.
- This emerges, for example, as Six Degrees of Separation, wherein we may connect any two nodes in a (social) network using a path of only six vertices.
- Note: Real networks are not Poisson so most real networks are not small world networks .
Ultra Small World
- A network has the ultra small world property if the average distance grows significantly slower than a regular small world network.
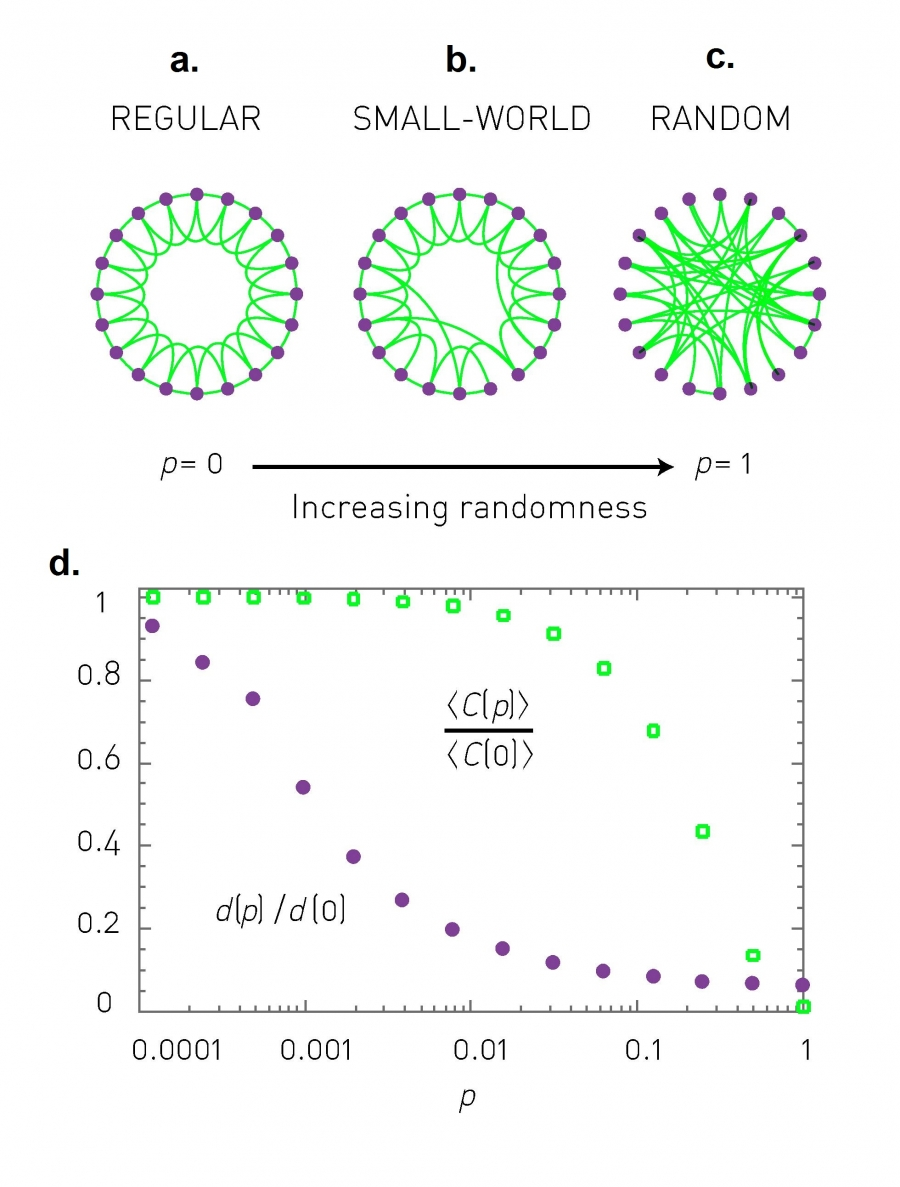
Watts-Strogatz Model
-
The Watts-Strogatz Model is a model for generating a small world network
-
We may generate a small network via the Watts-Strogatz model as follows.
- Start with a ring of nodes, each node connected immediately to their neighbors.
- With a rewiring probability
, we may choose to reconnect each link to a new pair of endpoints.
-
Effectively, then, the average distance and the average clustering coefficient depend on the rewiring probability
.