Preferential Attachment

• Preferential Attachment pertains to a phenomenon where new nodes prefer to link to more connected nodes.

• Preferential Attachment can be measured. The relative change of degree over time follows

• The empirical preferential attachment is measured based on the real network.

  • We can measure the preferential attachment when we know the time in which each node joined the network, or we have two snapshots of the network collected at not too distant moments in time.
  • Say we have two snapshots, the first at and the second at . For nodes that have changed degree during the time frame, measure , which is the relative change of the degree of node .
  • We can approximate with .

• The Cumulative Preferential Attachment Function is a function that shows the sum of empirical preferential attachments of each node added before node .

Degrees of Preferential Attachment §

• Preferential Attachment exists in various degrees. It exists based on the coefficient
  • Sublinear occurs in random networks
  • Linear which occurs in scale-free networks. This acts as a phase transition
  • Superlinear which shows up for hub and spoke networks.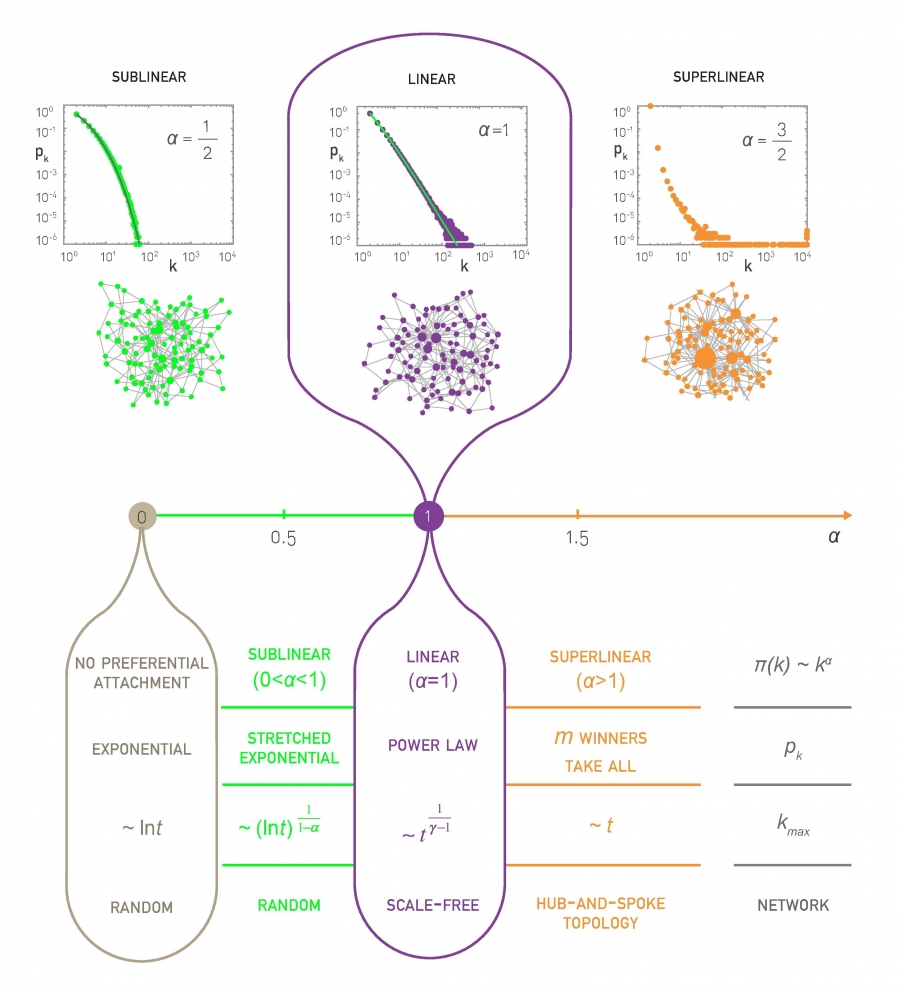

Sublinear §

• We observe the following when

• New nodes favor the more connected nodes. However, this bias is weak and not enough to make the network scale free

• The degree distribution follows an exponential distribution

  Where depends weakly on and we have a dependency on the average degree.

• Hubs are limited in size and number.

• The size of the largest degree varies logarithmically

  This also implies hubs grow slower.

Superlinear §

• When , we observe the following

• Almost all nodes connect to a few super-hubs. Especially apparent when ..

• The size of the largest degree is given as

Models of Preferential Attachment §

• Many models that can show networks with preferential attachment is that preferential attachment appears to be a byproduct of large, complex networks regardless if we use randomness or rational choice to grow the network.

Copying Model §

• The Copying Model is a local mechanism that generates a scale-free network without explicitly using preferential attachment.

• To decide where a new node connects, randomly select a node corresponding to a “related” node. Then, follow a two-step procedure:

  • With probability , the new node links to
  • With probability choose an outgoing link of and link the new node to the link’s target. That is, connect to a neighbor of the target, not the target itself.

• Preferential attachment is seen in this network. Let be the number of nodes in the network.

  The probability of choosing any node is The probability of selecting a degree node via the second step is .

  Then, the probability that a new node connects to a degree node is given as

  Which has linear preferential attachment. This indicates that the network generated is indeed scale-free.

Link Generation Model §

• The Link Generation Model *generates Scale Free Network without explicitly using preferential attachment *.

  • At each time step, add a new node to the network.
  • Select a link at random and connect the new node to one of the two nodes at the two ends of the selected link.

• Even without explicit mention of preferential attachment, this model is still capable of generating preferential attachment.

• Linear preferential attachment is apparent.

Barabasi-Albert Model §

Optimization Model §

• The Optimization Model is a global mechanism which aims to explain the topology of networks based on rational choice.

• Suppose we have a cost function

  Where denotes the cost of an edge denotes the distance of the node from the first node of the network.

• Three phenomena can arise

  • If a hub and spoke network arises since connecting to the central node is prioritized
  • If ,, then the cost term dominates and each node connects greedily to minimize locale extrema, resulting in a random graph.
  • If , the generated network is scale-free because
    • We correlate an optimum to connecting with the central node. This center becomes a hub but also any node close to the center becomes a hub by virtue of connecting new nodes towards it.
    • Because we are optimizing, nodes tend towards the optima (i.e., the hubs). Thus, there is preferential attachment
    

Links §

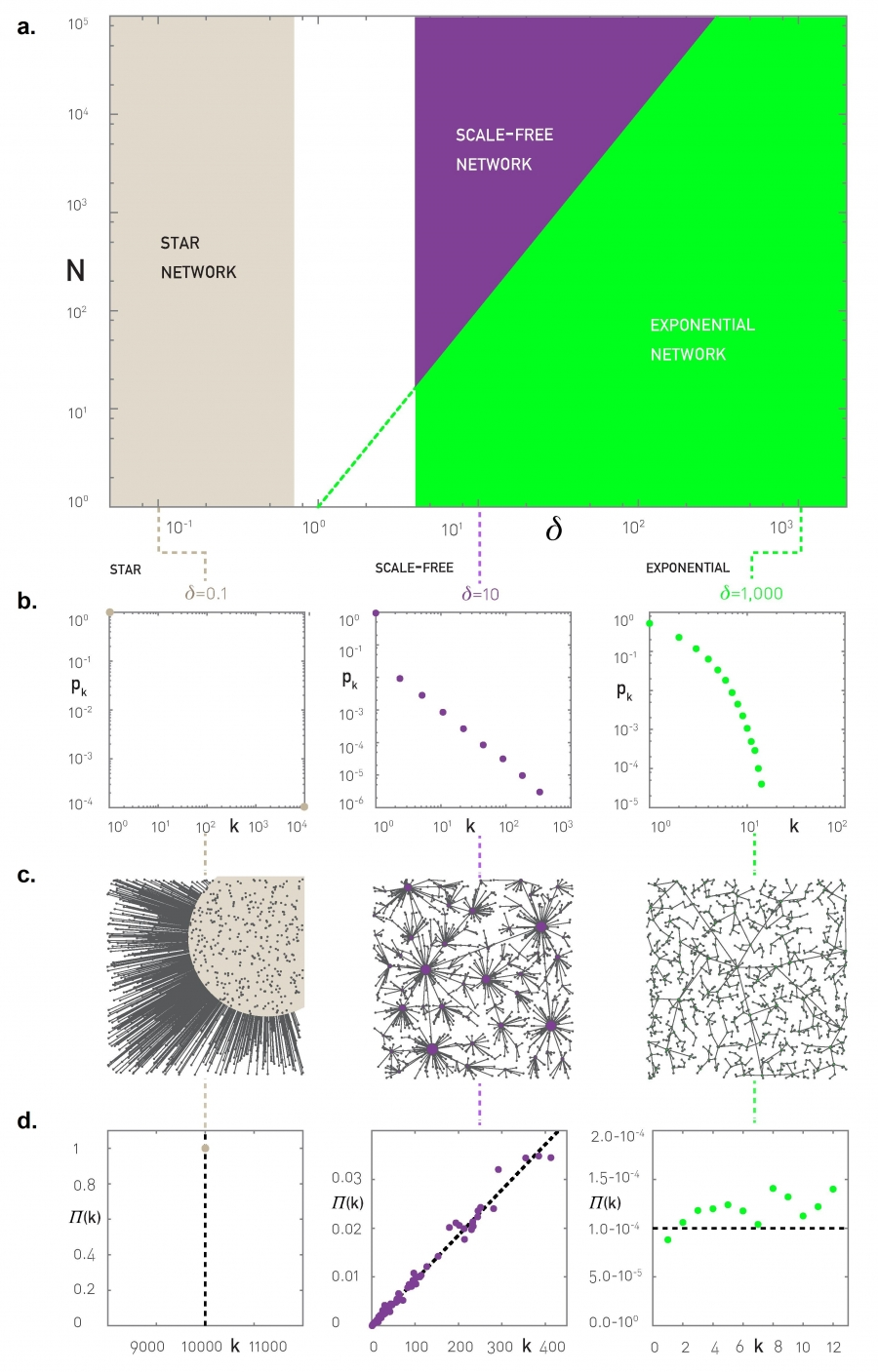
• Network Science by Barabasi
• Fundamental Constructs of Network Science