Epidemiology

• Epidemiology is not just applicable for diseases, it can also be applied to studying the spread of anything within a given population.

• A simple contagion assumes that the spread of a contagion requires only one contact between two entities

• A complex contagion assumes that the spread of a contagion requires more than one contact. The adoption of the contagion requires reinforcement.

  • This is applicable for modelling the spread of something memetic because the effect of the contagion is amplified with a larger contact surface.

Epidemic Models §

• The characteristic time is the time required for the number of infected to reach a fraction of .

• The Basic Reproductive Number of a disease, denoted is the expected number of susceptible individuals that are infected by an infected individual during the infectious period of a disease in a fully susceptible population.

  • It is the number of new infections each infected individual causes under ideal circumstances.

  • It is given by the formula

  • denotes the transmission rate, defined as the rate in which a disease spreads in a population. This is derived from two other parameters. The exact relationship is

  • - the number of contacts between persons in the population per unit time.

  • - the transmission probability — the risk of spreading the disease from infected to susceptible on contact.

  • denotes the recovery rate which is the rate in which an infected individual recovers from the disease.

  • is the spreading rate of the pathogen defined as

    The higher the spreading rate, the more likely the disease will spread.

    • The epidemic threshold is a threshold on the spreading rate that defines when epidemics become possible within the population

• characterizes various diseases

  • If , the infection is able to spread in a population.
  • If , the infection is unable to spread. It is said to be endemic.

Homogeneous Models §

• These models assume that a person has a comparable number of contacts within a social network. Thus:

  • Compartmentalization — each individual in the population can be classified into different categories which they can move through
  • Homogeneous Mixing - each individual has the same probability of coming into contact with other individuals

• Each model predicts the following

  • The early stages of an epidemic are characterized by an exponential growth in the number of infected.
  • The late stages of an epidemic is ultimately decided by the Basic Reproductive number — which also determines transmission and recovery rate.

• These models fail when the assumptions of compartmentalization and homogeneous mixing fail. For example, when applied to real networks

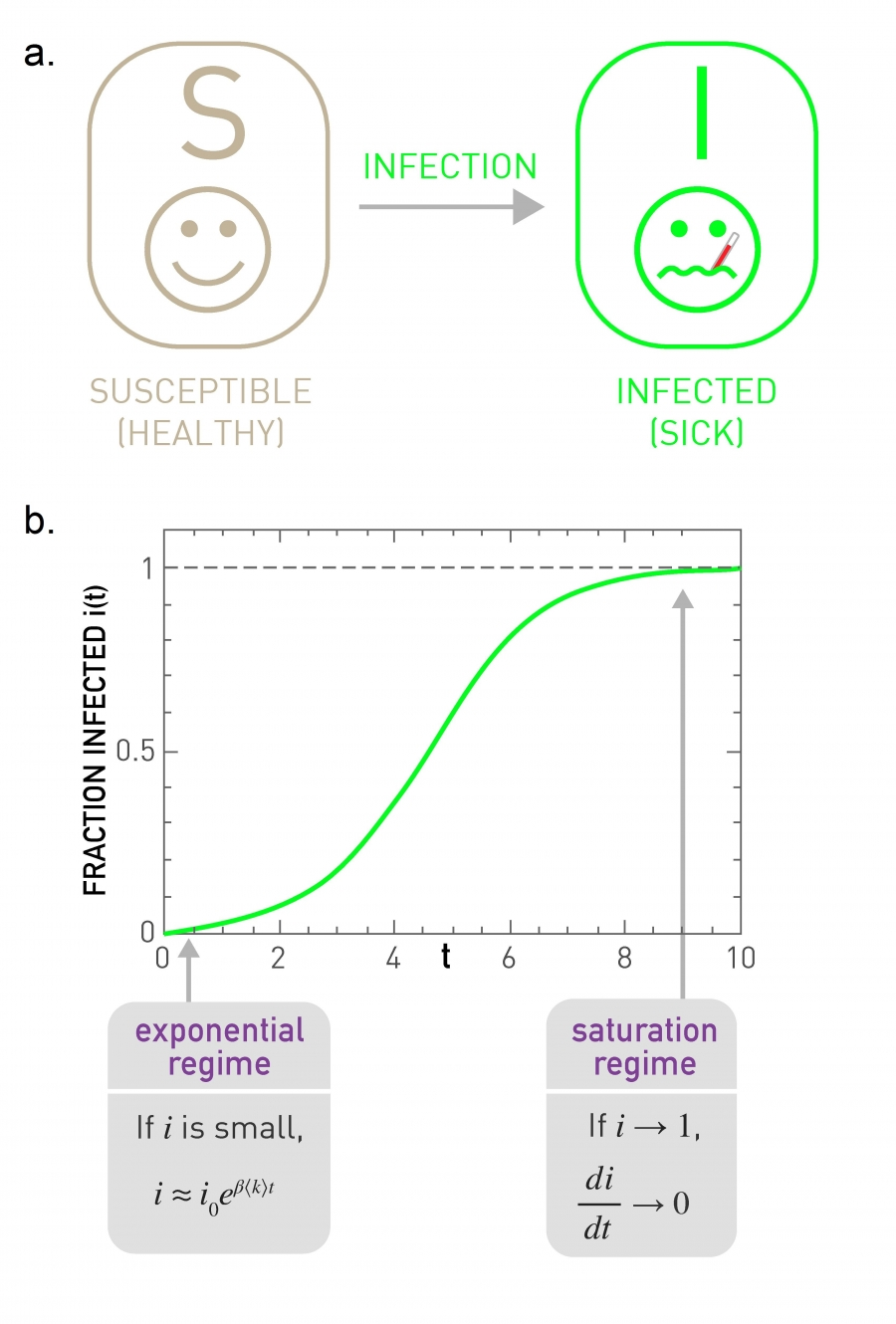
Susceptible-Infected §

• At time , we have and as the fraction of susceptible and infected individuals. At everyone is susceptible.

  • Any susceptible person has a chance chance of being infected , as well as an average number of contacts such that .

• The dynamics of the model is captured by the Differential Equation

• We observe the following:

  • The fraction of infected individuals varies with a logistic curve

    Where is the number of initial infected.

  • At the beginning, the fraction of infected individuals increases exponentially.

  • The characteristic time is given by

  • With time, an infected encounters fewer susceptible. Hence, the growth slows down for large .

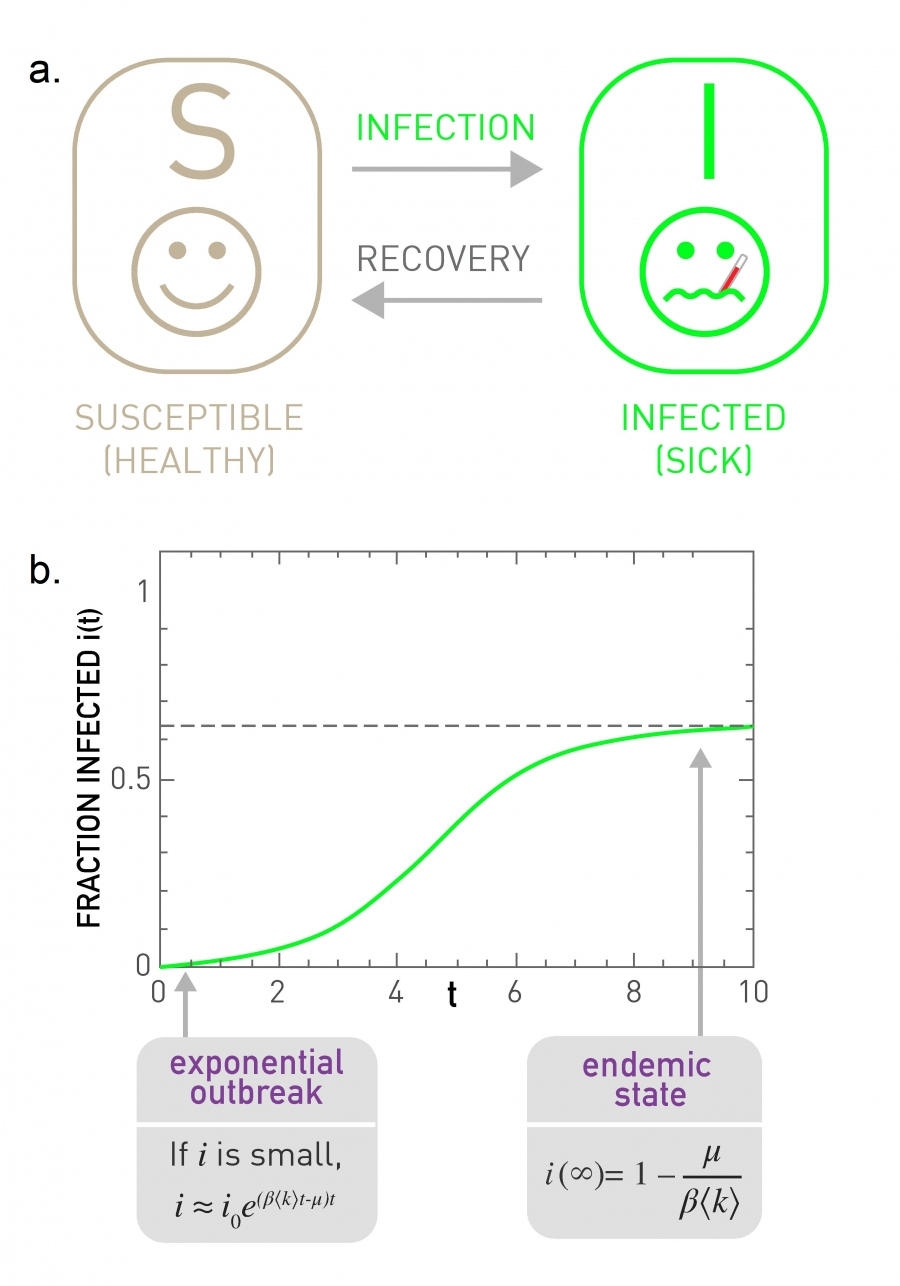
Susceptible-Infected-Susceptible §

• At time , we have and as the fraction of susceptible and infected individuals. At everyone is susceptible.

  • Any susceptible person has a chance chance of being infected , as well as an average number of contacts such that .
  • Any infected people can recover with probability .

• The dynamics of the model are given by the following differential equation

• We observe the following

  • he fraction of infected individuals increases as

    Where

  • We have two possible states

    • Endemic , the fraction of infected individuals follows a logistic curve. However, not everyone is infected, and we have only a finite fraction of the population infected.

      More specifically, the fraction of infected converges to when the number of infected equals the number of susceptible, or

      This is obtained by setting

    • Disease-free . For high recovery rates, decreases exponentially so that infection will die out

    Intuitively, this is because the number of individuals cured is more than the number of newly infected.

    The characteristic time is given by

Susceptible-Infected-Recovered §

• At time , we have , , and as the fraction of susceptible and infected individuals. At everyone is susceptible.

  • Any susceptible person has a chance chance of being infected , as well as an average number of contacts such that .
  • Any infected people can recover with probability . They become recovered and are removed from the population.

• The dynamics are given by the following differential equations

\frac{dS}{dt} &= -\beta \ I \ [1-(R+I)] \ \frac{dI}{dt} &= -\mu I + \beta \ [1 - (R+ I)] \ \frac{dR}{dt} &= \mu I \end{split}\end{equation}