Convolutional Neural Network

• A Convolutional Neural Network (CNN) is a class of Neural Network based on the use of convolutions that slide along input features to provide translation equivariant responses.
• It is typically used for structured input (commonly images).

Architectural Details §

• Convolutions were not chosen randomly, the choice to use a convolution is natural considering the following reasonable constraints that we want to impose upon an image in computer vision.

  • Equivariance - the “object-ness” of any particular object in the image remains the same regardless of any rotation, translation or scaling that is applied (i.e., it is invariant to certain symmetries)
  • Locality - pixels that are close to each other in the image tend to be related to each other.
  • The model should gradually capture long ranged dependencies by expanding its receptive field the deeper we go.

• We illustrate the above as follows

  Consider a network with internal representation . We may then write this internal representation with the weight matrix and the bias using the following equation, taking input .

  Where .

  Note that and are two dimensional.

  Now, we may invoke translational equivariance to simplify the equation by removing the dependency of with to get for constant :

  By locality, as well we my set if . for some appropriate

  Effectively, this procedure has reduced the number of parameters we need to store, at the cost of having to assume our assumptions above. We refer to as the convolutional kernel (even though the operation above really does cross-correlation).

  The last concern of deep layers being able to capture global information can be achieved through interleaving non-linearities and convolutional layers.

Convolutional Layer §

• A Convolutional Layer is a layer which performs the cross correlation (a.k.a. convolution) operation between the input and a convolution kernel then adds a bias.

  Let be the output of the convolutional layer be the input of the convolutional layer, assumed to be appropriately sized. be the convolution kernel of appropriate size be a scalar bias term.

  Then

• The kernel of a convolutional layer is a learnt parameter. That is, we update this kernel in the same way we update most parameters during training

• Strictly speaking, a convolutional layer does not perform any convolutions.

  • However, in practice this does not matter because cross-correlations and convolutions are equivalent.
  • In training it does not really concern us what elements in the input correspond to what elements in the kernel tensor.

• We typically see the use of Convolutional Blocks — modules which consist of convolutional layers plus additional Pooling.

• Convolutional layers can also be Batch Normalized. In which case, apply batch normalization after applying convolution and before feeding to the activation.

  • This is done per channel across all locations
  • Each channel will have its own scale and shift parameters, as defined in Batch Normalization.

1x1 Convolutional Layers §

• A 1x1 convolutional layer is one that uses a 1x1 convolution kernel.
• The result is that each computation only occurs in the channel dimension.
• Each output in the channel dimension corresponds to a Linear Combination of the inputs channels.
• Outputs and inputs correspond to exactly one pixel.
• It acts like a form of dimensionality reduction and a means to use activation functions to introduce a local non-linearity.

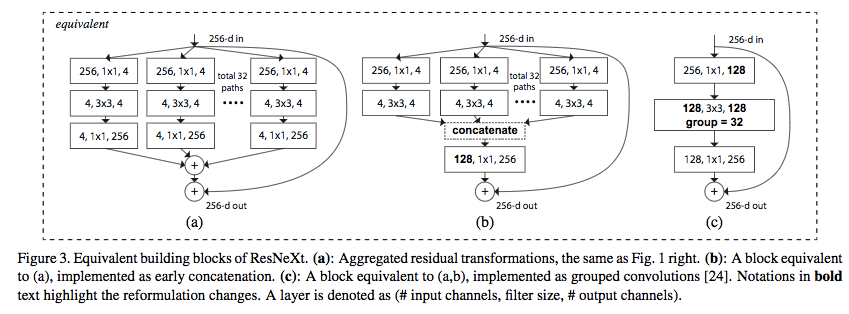
Grouped Convolutions §

• A Grouped Convolution uses a group of convolutions (multiple kernels per layer) to learn a varied set of low level and high level feature maps.

Grouped Convolution. Image taken from Zhang et al.

Key Features §

• Feature Maps pertain to the output of a convolutional layer. It can be regarded as the learned representation in the spatial dimension of the inputs

• Padding the input such that the resulting feature map will be the same dimensions as the original images helps address one issue where performing the cross correlation results in a slightly smaller image.

  • Typically this also means we want our kernels to have odd dimensions. That way, the amount of padding at the top and bottom remains the same.
  • Additionally, this also means that we can re-interpret the output of the cross correlation in the feature map to be the one where the convolution kernel window was centered at the corresponding cell in the input.
  • This has the added consequence of making sure each input is used equally frequently.

• Stride refers to the number of rows and columns traverse per slide of the window of a convolution kernel.

  • By default, we assume the stride is 1 across all dimensions. This is equivalent to sliding the kernel window to each cell.
  • If we cannot have the window fit after it has slid, we no longer perform the cross-correlation on the region.
  • We may want to increase the stride for two reasons:
    • Computational efficiency since we reduce the number of cross-correlation operations performed.
    • Downsampling

• If kernel has shape , the input image dimension , padding and stride , the output shape after applying the convolution is

  • If we have multiple channels, we assume the kernel has the same number of input channels as the input data. The output shape of the layer will then be where is the number of channels

Pooling §

• A pooling operation is an operation wherein a fixed size window (called the pooling window) is slide over all regions of the input based on the stride.

  • This is comparable to a convolution except that we do not have parameters corresponding to a kernel. Instead we perform some form of aggregation on the sub-region contained in that window.
  • It is intended to achieve a small amount of translational invariance
  • It can also be used for downsampling.

• Average Pooling is a pooling operation wherein we take the mean of all values contained within the pooling window.

  • We obtain a smoother output as a result.

• Maximum Pooling is a pooling operation wherein we take the maximum of all values contained within the pooling windows.

  • We extract the most pronounced features

• Global Average Pooling is a pooling operation designed to replace Fully connected layers within a Convolutional layer.

  The idea is to generate one feature map for each category of a classification task and instead of adding fully connected layers, we take the average of each feature map before feeding it directly to a softmax layer.

  • One advantage is that it is much closer to the convolution structure. It enforces correspondences between feature maps and categories. Feature maps can be interpreted as the confidence maps for categories.
  • It avoids overfitting because it does not require parameters to optimize.
  • It enforces Translational Invariance by summing out spatial information.

Links §

• Dive into Deep Learning by Zhang, Lipton, Li and Smola - Ch. 7.1
• The Evolution of Convolutional Neural Networks