Asymptotic Analysis

• When we are only concerned with the order of growth of a funnction at large input, we are studying the asymptotic efficiency. ^{1 2 3}

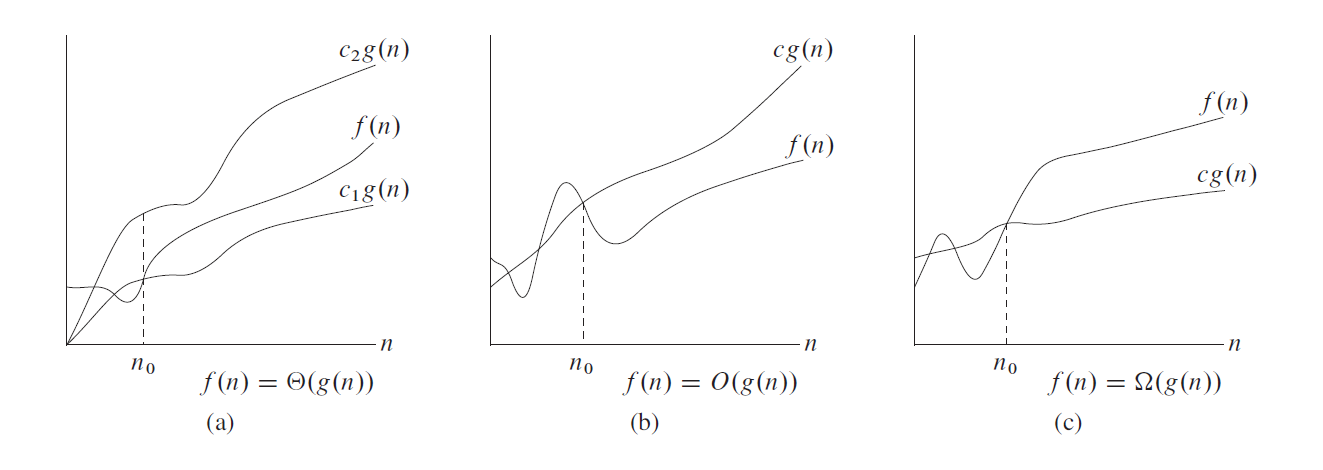
• For a given function , the asymptotic tight bound denoted is defined as

• For a given function , the asymptotic upper bound denoted is defined as

• For a given function , the asymptotic lower bound denoted is defined as

• For a given function , the strict asymptotic upper bound denoted is defined as

  Here becomes infinitesimally small relative to as .

• For a given function , the strict asymptotic lower bound denoted is defined as

  Here becomes arbitrarily large relative to as .

• An alternative definition can be formulated by considering .

• CLRS 3.1 For any two functions and we have that

• The asymptotic functions above define equivalence on the space of functions

• Some additional rules

Asymptotic Analysis. Image taken from Cormen, Leiserson, Rivest, and Stein

Links §

• CLRS

Footnotes §

1. These can be used to analyze other functions as well. However, do note that we implicitly assume that for large enough , the function becomes non-negative. ↩

2. When we say we implicitly mean . ↩

3. Another way to read the definitions is that the only way for to compare to is if it is scaled by an appropriate constant . ↩