Constructible Numbers
- A real number
is constructible if we can construct a line segment of length in a finite number of steps from a given segment of unit length given a straightedge and compass. - (Fraleigh 32.1) If
and are constructible real numbers, then so are , , , and if , . See the constructions below

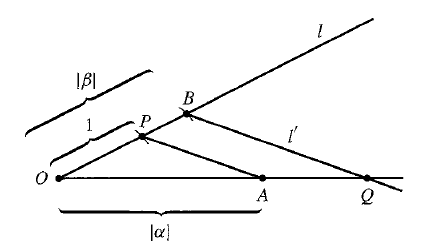
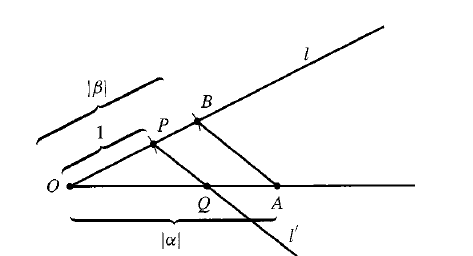
- (Fraleigh 32.5) The set of all constructible real numbers forms a subfield
of the field of real numbers. - (Fraleigh 32.6) The field
of constructible real numbers contains precisely of all real numbers that we can obtain from by taking square roots of positive numbers a finite number of times and applying a finite number of .
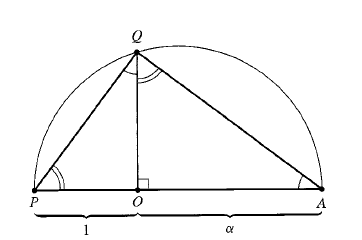
-
(Fraleigh 32.8) If
is constructible and , then there is a finite sequence of real numbers such that is an extension of of degree . In particular for some integer -
(Fraleigh 32.9) Doubling the Cube is impossible. Given a side of a cube, it is not always possible to construct with a straightedge and compass, the side of a cube that has double the volume of the original cube.
- Proof: Doubling a cube requires the construction of the cube root, which is impossible unless
is a power of
- Proof: Doubling a cube requires the construction of the cube root, which is impossible unless
-
(Fraleigh 32.10) Squaring the Circle is Impossible. Given a circle, it is not always possible to construct with a straightedge and compass, a square having area equal to the area of the circle.
- Proof:
is transcendental over and also not representable using square roots. Therefore it is not constructible.
- Proof:
-
(Fraleigh 32.11) Trisecting the angle is impossible. There exists an angle that cannot be trisected with a straightedge and compass.
- Proof: The angle
, if trisected, gives . But, it can be shown that requires the use of cube roots to construct, which is impossible unless is a power of .
- Proof: The angle