Dynamic Games of Complete Information

Nash Equilibrium §

• The principles applied here are applicable in the analysis of dynamic games of complete information since we can convert extensive-form to normal-form (see here). In doing so, we can capture all the Nash Equilibria of the dynamic game.

  • In an extensive game, every outcome of the game is associated with a unique path of play determined by some Nash Equilibrium in the game.

    More formally, let be a Nash equilibrium profile of behavioral strategies in an extensive form game. An information set is on the equilibrium path if given it is reached with positive probability ¹.

    An information set is off the equilibrium path if it is never reached.

• In a Nash Equilibrium, players choose to proceed on the equilibrium path because of their beliefs about what the players are doing on and off the equilibrium path.

  • However, because normal-form games treat all choices as “once-and-for-all” simultaneous choices, beliefs can never be challenged and the player may not respond optimally
  • Players only act rationally on the equilibrium path based on the belief on what happens both on and off the equilibrium path. However, there is no restriction on the beliefs of players off the equilibrium path.
  • This is in contrast to what we might expect where players can respond optimally wherever they are called to move.

Sequential Rationality §

• Given strategies , we say that is sequentially rational if and only if is playing a best response to in each of his information sets.

• A backward induction procedure is one where we start from the terminal nodes at the end of the game and work our way up the decision tree to its root.

  • (Tadelis 8.1) Zermelo’s Theorem- Any finite game of perfect information has a backward induction solution that is sequentially rational. Furthermore if no two terminal nodes prescribe the same payoffs to any player then the backward induction solution is unique.
  • (Tadelis cor. 8.1) Any finite game of perfect information has at least one sequentially rational Nash equilibrium in pure strategies. Furthermore if no two terminal nodes prescribe the same payoffs to any player then the game has a unique sequentially rational Nash equilibrium.

• Backward induction cannot be applied to games of imperfect information, nor to games that do not end in finite time.

Subgame-Perfect Nash Equilibrium §

• A proper subgame of an extensive-form game consists of only a single node and all its successors in with the property that if and , then . The subgame is a game tree that is a subtree of .

  • In other words, it is a smaller game within the larger game.
  • A player’s best response depends only on his beliefs about what the other players are doing within the subgame

• Let be an -player extensive form game. A behavioral strategy profile is a subgame-perfect Nash equilibrium if for every proper subgame of , the restriction of to is a Nash equilibrium in .

  • is a Nash equilibrium in all subgames, even those that are not reached in the equilibrium path.

• For any finite game of perfect information, the set of subgame-perfect Nash equilibria coincides with the set of Nash equilibria that survive backward induction.

• At least one of the Nash equilibria in a game will be a subgame-perfect equilibrium.

• In other words, to check if is a subgame-perfect equilibrium, we need to show that for every player , given , player does not have a single information set from which he would want to deviate .

Multistage Games §

• A multistage game can be viewed as an extensive-form game.

• Players should anticipate future games and use them to create a richer environment for themselves

• Players will benefit from using future play to create incentives that constrain their behavior in earlier stages.

• (Tadelis 9.1) Consider a multigame with stages, and let be a Nash equilibrium strategy profile for the -th stage game. There exists a subgame-perfect equilibrium in the multistage game in which the equilibrium path coincides with the path generated by . ²

  • If we look at a sequence of plays that is a Nash equilibrium in each game independently then players should be content playing these stage-game strategies in each stage-game. Each stage game can be treated as if they were independent games.

• (Tadelis 9.2) If is a Nash equilibrium of the multistage game consisting of as stage games, then the restriction of to the stage-game in period must be a Nash equilibrium of that stage .

  • In the last stage game, the players must play a Nash Equilibrium of that stage game. This follows from the fact that there is no future that can depend on the last action, ergo, the players should play a Nash Equilibrium

• (Tadelis 9.3) If a finite multistage game consists of stage-games that each have a unique Nash equilibrium then the multistage game has a unique subgame-perfect equilibrium.

  • Because of (Tadelis 9.2), we must have that the penultimate game must also be independent of the future (since the next game is independent of the future) and so the unique Nash Equilibrium of that stage must be played.

• A Nash Equilibrium need not be played in the early stage games when:

  • There must be at least two distinct equilibria in some middle stage, a carrot (reward) and a stick (punishment)
  • The discount factor has to be large enough for the difference in payoff between the carrot and the stick to have enough impact in the first stage of the game. Long term losses must outweigh short term gains.

One Stage Deviation Principle §

• A strategy is optimal if there is no strategy such that

• A strategy is one-stage improvable if there is no information set , action and corresponding strategy such that

• (Tadelis Thm. 9.1) One Stage Deviation Principle A one stage unimprovable strategy is optimal

  • Intuition: If were not optimal, then we can find deviations that improve it. Because the game is finite, having finite strategies, the sequence of deviations performed must terminate.

• In other words: if no player can increase their expected payoff by deviating from their original strategy via a single action (in just one stage of the game), then the strategy profile is a subgame-perfect equilibrium.

Repeated Games §

Finitely Repeating Games §

• (Tadelis 10.1) If the stage-game of a finitely repeated game has a unique Nash equilibrium, then the finitely repeated game has a unique subgame-perfect equilibrium. ³

• Because it is common knowledge that the game will end, players will not have the rewards and punishment incentives. At the very last game, they can choose to maximize their profits and this effect cascades all the way to the beginning of the game.

Infinitely Repeating Games §

• A profile of pure / behavioral strategies , is a subgame-perfect equilibrium if the restriction of is a Nash equilibrium in every subgame.

  That is, for any history of the game is the continuation play dictated by the strategy profile is a Nash Equilibrium.

• (Tadelis 10.2). Let be an infinitely repeated game, and be a static Nash equilibrium strategy profile of the stage-game .

  Define the repeated-game strategy for each player to be the history-independent Nash strategy for all .

  Then is a subgame perfect equilibrium in the repeated game for any ⁴

• We can use a subgame-perfect equilibrium to support itself. That is, the very knowledge of the subgame-perfect equilibrium is enough to support itself. We call such equilibria bootstrap equilibria
• Grim trigger strategies - a strategy wherein the player cooperates for as long as other players have cooperated. After which, if any player has deviated in the past, the player deviates permanently.
  • The grim trigger is itself an incentive for players to cooperate long-term and to ignore short-term temptations.
  • In effect, the payoff captures not only the reward today, but the reward for maintaining the status quo.
  • If the players are patient (high enough ) there is a reward-and-punishment strategy that keeps them cooperating forever. If the future is certain to end, then the players will deviate at no repercussion.
• (Tadelis 10.3) In an infinitely repeated game a profile of strategies is a subgame perfect equilibrium if and only if there is no player and no single history for which player would gain from deviating from . ⁵

• (Tadelis Thm 10.1) The Folk Theorem. Let be a finite, simultaneous-move game of complete information. Let denote the payoffs from a Nash Equilibrium of and be a feasible payoff of (that is, a payoff achieved by combinations of stage game strategies).

  If and if is significantly close to , then there exists a subgame-perfect equilibrium of the infinitely repeated game that achieves an average payoff arbitrarily close to . ⁶

Reputation §

• We can re-interpret the need for high discounting and an uncertain terminal period (necessary for infinitely repeating games) in a variety of ways.

• Cooperation as Reputation. Players in a repeated relationship can create a reputation to cooperate with each other. Sudden uncooperative behavior is rewarded with a grim-trigger strategy.

• A third-party can be used as a reputation mechanism. The idea is that this third party will be able to sustain the reputation for supporting the good behavior of others since he is incentivized to do so. They can then be used to enforce good behavior because they are established as trustworthy.

• Reputation can be transferred without third parties - Reputation acquired under the name of a firm or entity may be separated from the identity of the player who is operating under the firm’s name. ⁷

Example Games §

• The Centipede Game

Centipede Game

* Based on empirical experiments with the game: When players are expected to share common knowledge of rationality they indeed play the backward induction solution.

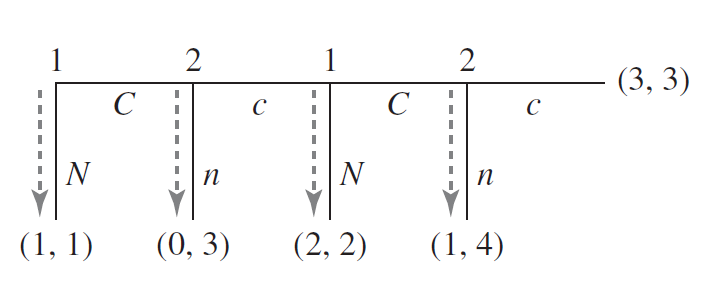
• Stackelberg Model of Duopoly - a sequential version of the Cournot game wherein price is fixed and quantity is set. The only difference is firm 1 chooses first before firm 2.

• Tacit Collusions - an infinitely repeated game played by two firms wherein they must tacitly agree to share the rewards from holding a shared monopoly. It illustrates two things:

  • If the two firms can agree to a game-theoretic view, they can circumvent any explicit rules against collusion.
  • Price wars between colluding firms are off-the-equilibrium path behavior that occurs when collusive behavior is no longer a subgame-perfect equilibrium (i.e., due to uncertainty in the other players’ tacit agreement ).

Strategic Bargaining §

Links §

• Tadelis Ch. 7 - 11.
  • 10.4 - an application of Infinitely repeated games - namely Tacit Collusion
• Game Theory - Strategy

Footnotes §

1. Analogous to support ↩

2. This follows from the fact that current play does not affect future play. ↩

3. A special case of Tadelis 9.3 ↩

4. Follows similar logic to Tadelis 9.1. Future behavior of opponents is independent of history so history has no role for current play. ↩

5. Logic follows from Tadelis Thm 9.1. We have two states- the norm and the deviation. The deviation state is a trap state. ↩

6. The intuition is that the payoff vector, which is in the convexex]] hull, is a weighted average of some combination of payoffs that result from pure-strategy profiles. We can then construct a sequence of strategy profiles that will imitate the weights required to achieve . A reward-and-punishment strategy is possible because . A high enough discount factor discourages players from deviating. ↩

7. Hence even just the reputation of a good name can do wonders for a brand ↩