A Generative Adversarial Network relies on the following principle: a data generator is good if we cannot tell fake data from real data.

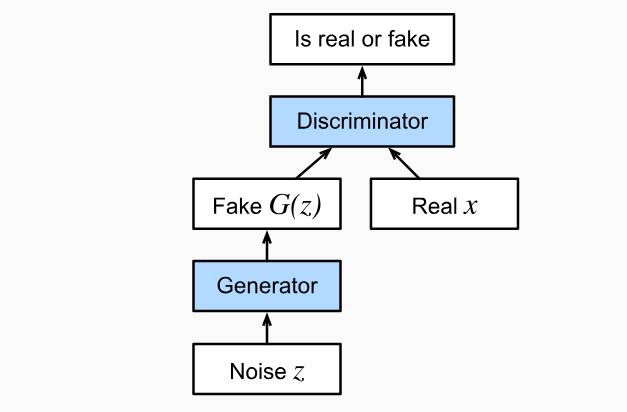
Generative Adversarial Network pipeline. Image Taken from Zhang

The GAN architecture requires two parts
- A generator that can generate synthetic data that looks like real data. It draws a latent variable from a source of randomness ¹ . It then applies a function to generate
- A discriminator that can distinguish real data from fake data. It is a binary classifier that can distinguish if is from real data or from the distribution.

In the GAN architecture, both networks are in competition with each other.
- The generator wants to fool the discriminator.
- The discriminator wants to detect the fake data.

Training

Training involves alternating between training and :
- is trained for one or more epochs, keeping fixed. In this way, learns to detect the flaws of .
- is trained for one or more epochs, keeping fixed. In this way, learns to fool .
- Repeat.
Over time, ’s performance gets worse because the ’s accuracy (assuming gets better) converges to . This means that feedback for (which comes from ) gets worse over time and ’s performance might soon become random too. Convergence is unstable.
and are playing a minimax function with the objective function called the minimax loss (which derives from Cross Entropy Loss)

There are two issues with this:
- Vanishing Gradients
- Mode Collapse wherein the generator does not generalize. Instead, it generates a limited number of outputs — specifically the ones that seem most plausible to the discriminator. As a result, the discriminator only learns to reject those outputs.
An alternative loss that can be used is the Wasserstein Loss function. We modify the GAN to be a Wasserstein GAN (WGAN) where the discriminator outputs a larger number (possibly greater than ) for real instances than for fake instances.

We call the discriminator of WGAN a critic. The loss function is defined as follows

An important requirements for WGAN is that weights need to remain within a constrained range;

The Library