Binary Search Tree
-
A binary search tree is a binary tree organized to satisfy the binary-search tree property:
Let
be a node in a binary search tree. If is a node in the left subtree of , then . If is a node in the right subtree of , then -
By convention, all leaves have
NILvalues.
Operations
-
Traversal across the tree takes
time. - The binary search tree property allows us to print all keys in sorted order. This is called inorder traversal
if x != null INORDER(x.left) print(x.key) INORDER(x.right)- We can also print the root before the values in either subtree. This is preorder traversal
if x != null print(x.key) PREORDER(x.left) PREORDER(x.right)- We can also print the root after the values in either subtree. This is postorder traversal
if x != null PREORDER(x.left) PREORDER(x.right) print(x.key) -
A binary search tree is often used to perform
SEARCHoperations. Search can be done intime where is the height of the tree. Extensions of search are also time. - The
MINIMUMof the tree is the left most node. - The
MAXIMUMof the tree is the right most node. - The
SUCCESSORof a nodeis given as follows: - If the right subtree of
is not empty, the successor is the leftmost node in ’s right subtree. - If the right subtree of
is empty and has a successor, then is the lowest ancestor of whose left child is also an ancestor of
- If the right subtree of
- The
PREDECESSORof a nodeis given as follows. - If the left subtree of
is not empty, the predecessor is the rightmost node in ’s left subtree. - If the left subtree of
is empty and has a predecessor, then is the lowest ancestor of whose right child is also an ancestor of .
- If the left subtree of
- The
-
INSERTis given by inserting a new nodein the tree such that the binary search property is maintained. Insert takes - To find where to place
we simply perform a traversal until we reach a leaf and then insert either to the left or to the right of depending on the values of their keys. - If
is the first node to be inserted in the tree, also becomes the root.
- To find where to place
-
DELETEfor nodein Binary Search Tree must handle three cases. Delete takes - If
has no children, simply remove it from the tree. Modify the parent accordingly. - If
has one child, elevate that child to take ’s position in the tree by doing z.parent.child = z.child, where child is left ifz.childwas a left child and right otherwise. - If
has two children, first find ’s successor . must lie in ’s right subtree and must have no left children. Splice out of its current location and have it replace . - If
is ’s right child, replace by . - If
is not ’s right child, replace by its own right child and then replace by . 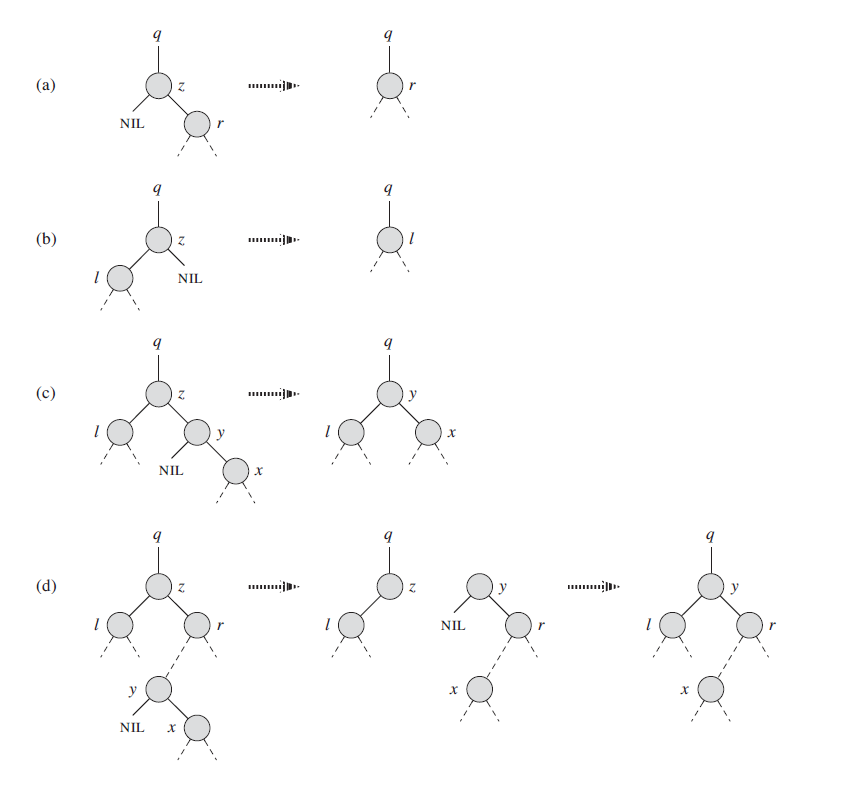
- If
- If
- Rotation is a local operation that preserves the Binary Search Tree property but changes the pointer structure
LEFT ROTATION(x): Supposeis any node such that its right child is not NULL. We pivot around the link fromto so that is the new root of the subtree, with as ’s left child, and ’s left child as ’s right child. RIGHT ROTATION(x):Supposeis any node such that its left child is not NULL. We pivot around the link fromto so that is the new root of the subtree, with as ’s right child and ’s right child as ’s left child. 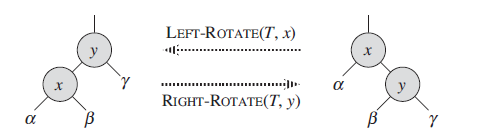
Properties
-
Assuming a balanced binary search tree, the height
is . -
(CLRS 12.4) The expected height of a randomly built binary search tree on
distinct keys is . 1
Red-Black Trees
-
A red-black tree is a binary search tree with one extra bit of storage per node for the node’s color. In particular
- Every node is either red or black
- Every leaf has
NILand is black - If a node is red, then both its children are black
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
-
A red-black tree ensures no path from the root to a leaf is twice as long as any other so that the tree is approximately balanced.
-
(CLRS 13.1) A red black tree with
internal nodes has height at most . - An immediate consequence of this is that any BST operation that takes
time takes time.
- An immediate consequence of this is that any BST operation that takes
Operations
- The regular
INSERTandDELETEoperations in BST cannot be directly adapted to Red-Black Trees because any such operations may break the red-black property.
Insert
-
During
INSERTof node, we set its color to be red. We then fix the tree since it may violate the Red-Black property. This still takes time. -
We maintain the following invariants:
- The variable
representing the current node , initially the inserted node, is made variable running through the loop is red at the beginning of each iteration. - All red nodes do not have red children except for possibly
and its parent . - All other properties are satisfied throughout the tree.
- The variable
-
Case 1:
’s parent is black. In which case we do not need to do anything. -
Case 2: Both
and the uncle are red. In which case we can repaint them black and the grandparent becomes red. Since
may now induce a red-red violation, we do . 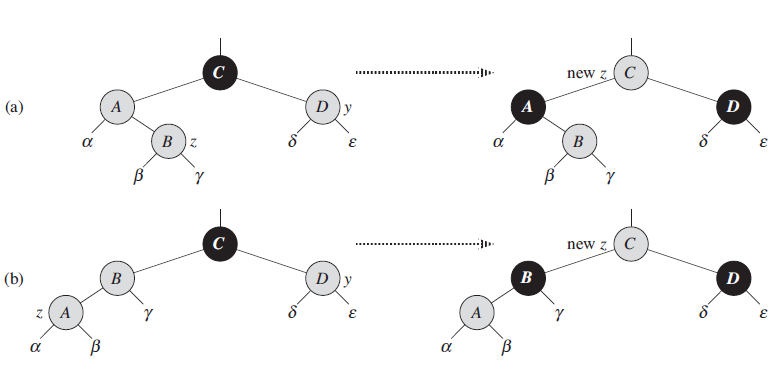
-
Case 3: The total height of the tree has increased by
. The current node is the red root of the tree. -
Case 4:
is red and the root. Switch ’s color -
Case 5:
is red but the uncle is black. is either or . Rotate to the grandparent position and proceed to Case 6 with -
Case 6:
is the left-left child or right-right child of . Let dirbe either left ifis left-left and right otherwise. Perform a rotation in the opposite direction at such that is in ’s position is the parent of and . 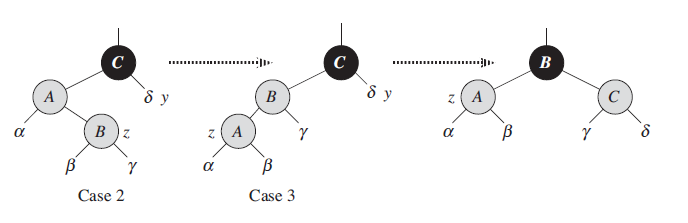
Delete
-
We cannot use the
DELETEprocedure of a regular Binary Search Tree since we may violate the Red-Black property. The overall run time for this procedure is. -
We consider, first, the simple cases. Let
be the deleted node. - If
has 2 children, swap its value with the in-order successor and then delete the successor instead. - If
has child, replace the node with its child and color it black. - If
has no children and is the root, replace it with NULL. - If
has no children and is red, remove the leaf node. - If
has no children and is black, remove it but make sure to fix the tree to rebalance it.
- If
-
When rebalancing the tree, we maintain the following invariants
- At the beginning of each iteration, the black height of
equals the iteration number minus one. - The number of black nodes on the paths through
is one less than before the deletion, whereas it is unchanged on all other paths. There is a black-violation at if other paths exist. - All other properties are satisfied throughout the tree
- At the beginning of each iteration, the black height of
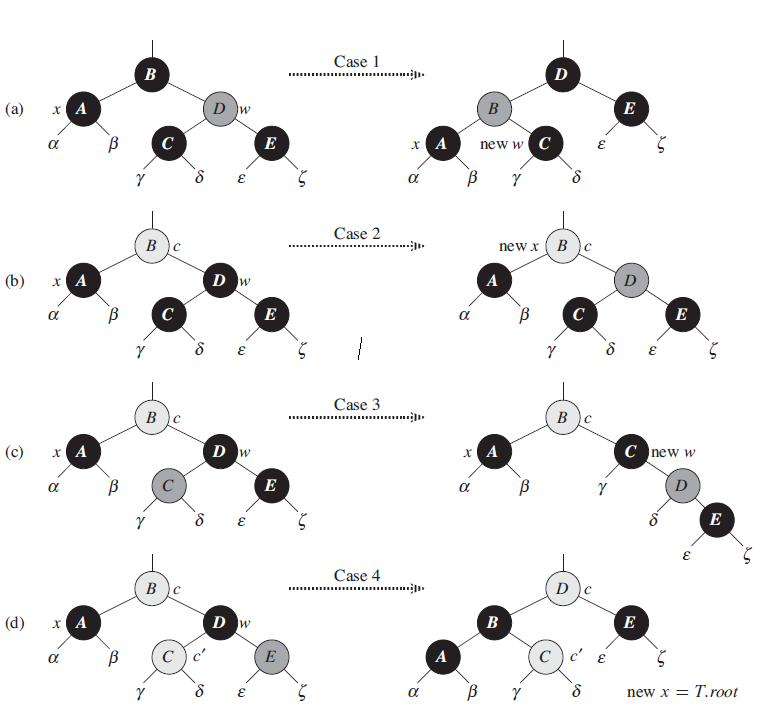
-
Case 1:
is the new root. The black height decreases by and we do not need to do anything else. -
Case 2:
and ’s children are black. Paint red and since we may violate the red-black property. We rebalance one black level higher. -
Case 3: The
dir-siblingis red and so and nephews have to be black. Perform a dir-rotation atso that becomes ’s grandparent and reverse the colors of and then proceed to Cases 4, 5, 6. -
Case 4;
and ’s children are black but is red. Change the colors of and to be red and black respectively. This makes up for our deleted black node. -
Case 5 :
dir-siblingis black. ’s close child is red and ’s distant child is black. Do a (1-dir)-rotation atso that becomes ’s parent and ’s new sibling. Exchange the colors of
and . has a black sibling whose distant child is red so we proceed to Case 6. -
Case 6 :
dir-siblingis black, ’ distant child is red. Do a dir-rotation atso that becomes the parent of and . Exchange the colors of and and make black. Paths not passing through
pass through the same number of black nodes has one additional black ancestor so the path passing through pass through one additional black node.
-
(CLRS 14.1). Red black trees can be augmented.
Let
be an attribute that augments a red-black tree of nodes and suppose that the value of for each node only depends on the information in nodes xx.leftandx.right, possibly includingx.left.fandx.right.f. Then, we can maintain the values ofin all nodes of during insertion and deletion without asymptotically affecting the performance of these operations Intuition: Any change to
only propagates to the ancestors of a node.
Order Statistic Trees
-
An order statistic tree is a red-black tree with additional information. Each node stores a “size” attributed. The size contains the number of internal nodes in the subtree rooted at
including itself. -
To retrieve the rank of any element in the tree, we do the following
First calculate the rank of
in the subtree it is rooted in. This is given as the size of its left subtree + 1 (to include itself). If the input rank is also equal to its rank in the subtree we are done Otherwise, traverse the left subtree with call
SELECT(x.left, i)if. This follows because we know the targeted node is to the left by the Binary Search property Otherwise, if
traverse the right subtree with call SELECT(x.right, i - r). Here, we know that the node must lie to the right and we “prune” out the other nodes and only consider the current subtree. This prunes outnodes hence our adjusted rank is . -
To maintain the subtree sizes during insertion and deletion, we simply increment or decrement the sizes of all affected parent / children nodes. This takes
time. When we adjust the tree with rotation, at most two nodes are affected. We adjust the sizes of these nodes accordingly.
Interval Trees
-
An interval is defined using a pair of real numbers
. is called the low endpoint and the high endpoint. Intervals
overlap if . -
Any two intervals satisfy the interval trichotomy. Exactly one of the following must be true
overlap is to the left of ’ is to the right of ’
-
An interval tree is a red-black tree where each element contains an interval. New intervals can be inserted, deleted or queried.
To facilitate better search operations, we maintain for each node
xthe valuex.maxwhich denotes the maximum value of any interval endpoint stored in the subtree rooted at. x.maxis maintained via the following relationx.max = max(x.int.high, x.left.max, x.right.max) -
In order to search for an interval that overlaps
, we do the following

-
(CLRS 14.2) Any execution of
INTERVAL-SEARCH(T,i)above either returns a node whose interval overlapsor returns NULLif no such interval exists.Proof Idea: We use the invariant that if tree
contains an interval that overlaps , then the subtree rooted at contains such an interval.
Links
-
CLRS - Ch. 12, 13, 14
Footnotes
-
The proof for this relies on Jensen’s Inequality. ↩