B Tree

• A B-Tree is a balanced search tree designed to work on external memory. They minimize the number of O operations.

  More specifically it is a rooted tree of minimum degree where

  • Every node has at most children. A node is full if it has exactly this amount.

  • Every node except for the root and the leaves, has at least children.

  • The root node has at least two children unless it is a leaf.

  • All leaves appear on the same level at the tree height .

  • A non-leaf node with children contains keys sorted in non-decreasing order.

  • The keys of a node denoted separate the ranges of keys stored in each subtree. If is any key stored in the subtree with root then

• B-Trees have a large branching factor compared to BSTs. However, we can guarantee that every B-Tree has height .

• For B-Trees we assume that is so large that it cannot fit into memory at once. Any B-Tree algorithms keep only a constant number of pages in memory at any given time.

• Disk operations for B-trees are performed as follows. Let be a pointer to an object.

  • If is in main memory, we can immediately access them as usual.
  • If is not in main memory, then we must read the object into main memory before we can refer to its attributes.
  • Any changes to require us to perform a disk write operation
  • Any pages in memory no longer in use are flushed.

• (CLRS 18.1) If then for any -key B-tree of height and minimum degree ,

  • B-trees save a factor of compared to a standard Red-Black tree.

Operations §

• SEARCH is a generalization to the search done in a BST except with -way decisions. The ordering of the keys helps with searching.
• INSERT involves inserting new keys into existing leaf nodes. If the leaf node is full, we split the keys of at the median key into two nodes with only keys each. The median key then moves into ’s parent. If the parent becomes full, we repeat this process.
• SPLIT can be done in one pass by splitting any full nodes that we encounter while we traverse the tree.
  • Splitting is the only way a B-tree increases in height

B Tree Split. Image taken from CLRS

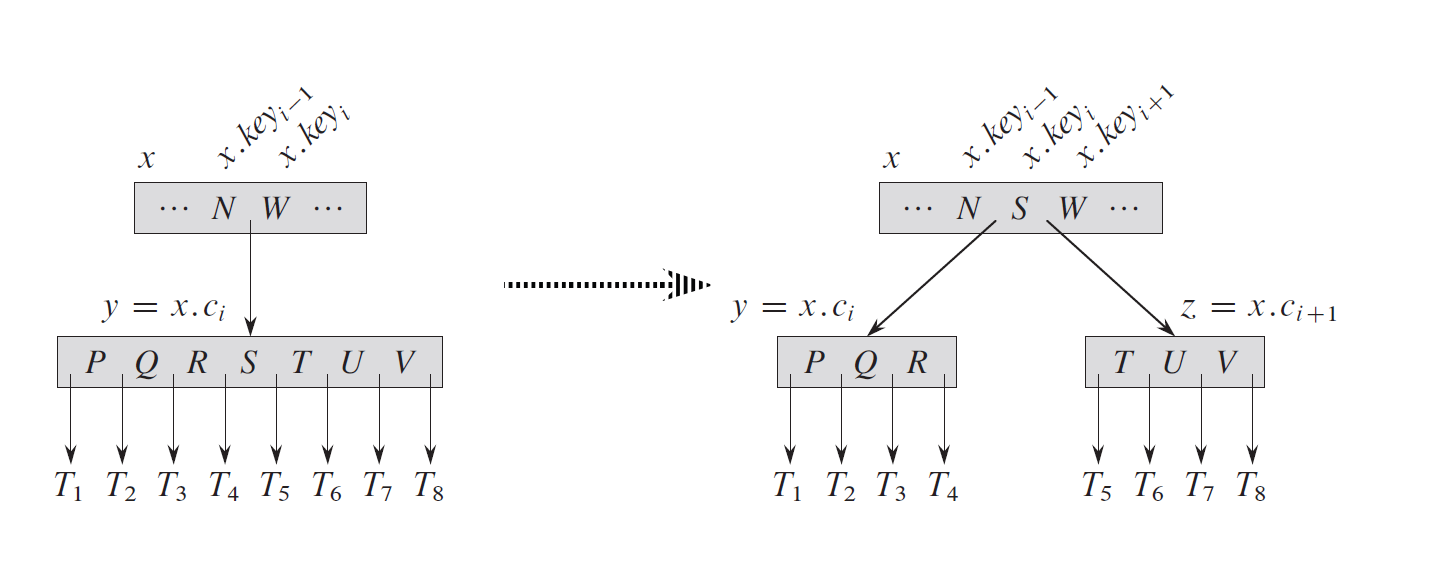
• DELETE involves not only removing a key from a node in the tree but also re-arranging the keys to preserve the B-Tree property.
  • If the key is in a leaf node, delete the key from .
  • If the key is in an internal node , the do the following
    • If the child that precedes in node has at least keys, find the predecessor of in the subtree rooted at . Recursively delete and replace by in .
    • If has fewer than keys then symmetrically examine the child that follows in node . If has at least keys then find the successor of in the subtree rooted at . Recursively delete and replace by in .
    • If and both have keys, merge and all of into so that loses both and the pointer to . now has keys. Free and recursively delete from .
  • If is not present, determine the root of the appropriate subtree that must contain . If has only keys, execute these steps.
    • If has only keys but has an immediate sibling with at least keys, give an extra key by moving a key from to , moving a key from ’s immediate left or right sibling up into and moving the appropriate child pointer from the sibling into .
    • If and both siblings have keys, merge with one sibling. Move a key from to the new merged node to become the median key for that note

B Tree Deletion Case 1, 2. Image taken from CLRS

B Tree Deletion Case 3. Image taken from CLRS

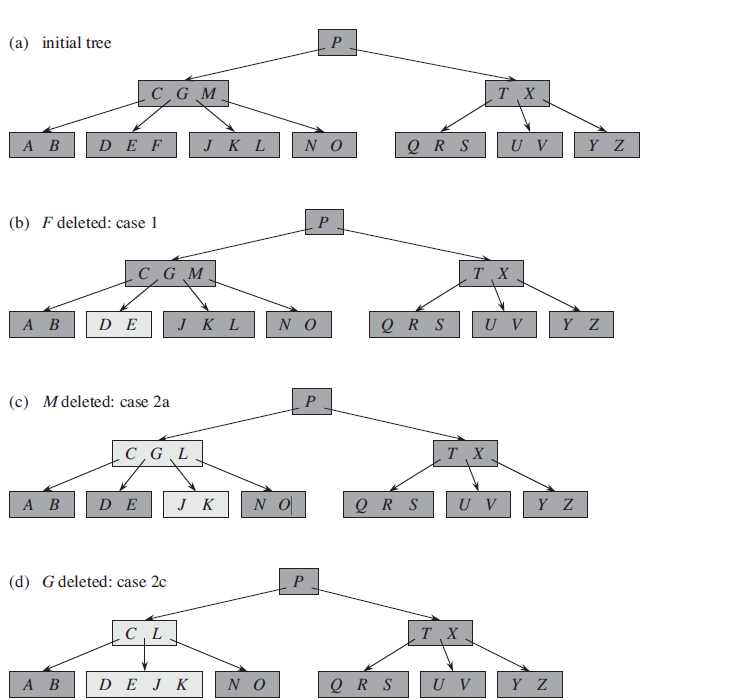
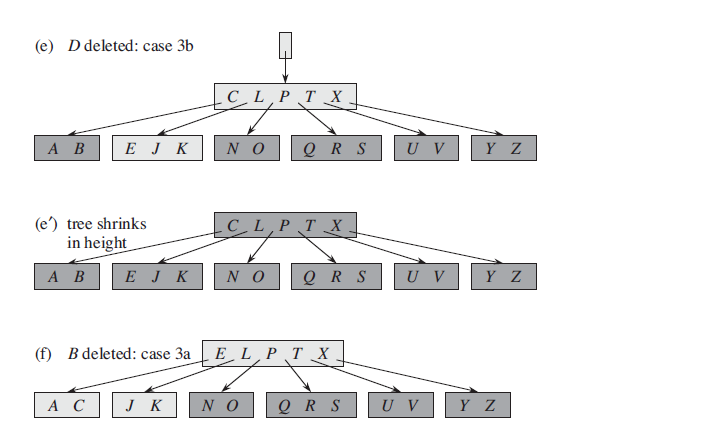
# Extensions * A **B$^+$-tree** extends a B-tree by storing only keys and child pointers in the internal nodes. Any auxiliary information is kept in disk and referred to with these pointer.

Links §

• CLRS - Ch. 18