Change of Variables
-
(see here. is independent of the coordinate system used for both and provided that both are connected to the Cartesian coordinate system by a diffeomorphic change of variables. Thus, diffeomorphisms can be used to transform an ODE to one we know how to solve through a change in variables.
-
The vector field on the
- axis with a unique component is denoted . This allows us to compute a diffeomorphism on a vector field - In general, let
be a fixed coordinate system in . Then the basis vector fields are denoted The vector field with componentsis denoted - Notice that the basis vector fields represent a change of coordinates matrix. If we have a given vector field, we can then obtain the vector fields in this coordinate system using matrix vector multiplication (which produces the sum above).
- Another way to write this is with the Jacobian Matrix
. Suppose we have functions and basis vector fields with DefineThen the change of variables is obtained as
- In general, let
-
(Arnold 5.3.1) Let
Are equivalent in the sense that if
Thus, the change of variables
- Proof: Verify that the proposed solutions are solutions
With
- Proof: Verify that the proposed solutions are solutions
-
To solve the differential equation
It suffices to construct a diffeomorphism that maps the direction field of the above to an equation we know how to solve.
-
Let
The image of the flow
For any
The orbits of
- Clearly the image
- (Arnold 5.5.1) The diffeomorphism
- Clearly the image
Integration
-
(Arnold 6.2.1.) Suppose a one-parameter group of symmetries of a direction field on the plane is known. Then the equation defined by this direction field can be integrated explicitly in a neighborhood of each nonstationary point of the symmetry group.
A point is called nonstationary for a transformation group if not all transformations of the group leave it fixed
-
(Arnold 6.2.2) In a neighborhood of every nonstationary point of action of a one parameter group of diffeomorphisms on the plane, one can choose coordinates
For sufficiently small
That is,
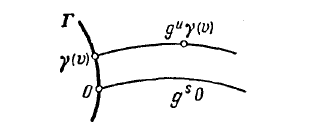
- Proof: This comes from the properties of group composition. In particular, consider the rectification below. Using a diffeomorphic mapping
- Proof: This comes from the properties of group composition. In particular, consider the rectification below. Using a diffeomorphic mapping
-
An equation is homogeneous if the direction field defining it on the plane is homogeneous; that is it is invariant with respect to the one parameter group of dilations.
- If
- Intuition: An equation is homogeneous if, when all variables are scaled by some constant, the equation remains the same (after cancellation).
- If
-
(Arnold 6.3.1) A homogeneous equation
Can be reduced to an equation with separable variables by the substitution
-
The function
-
(Arnold 6.3.2) Euler’s Theorem. A function is homogeneous of degree
Another way to say this:
-
Proof: In the forward direction, calculate
In the reverse direction, integrate the differential equation with separable variables defined by the Euler relation. That is, using
-
-
The homogeneous function of degree
-
A necessary and sufficient condition for the direction field of the differential equation
-
-
The
- This allows us to turn any algebraic curve with a singularity at the origin into a curve having no singularities except ordinary self-intersections.
-
A group of quasi-homogeneous dilations of the plane is a one-parameter group of linear transformations
We refer to
-
An equation is called quasi-homogeneous with weights
- (Arnold 6.4.1) A quasi-homogeneous equation
- (Arnold 6.4.1) A quasi-homogeneous equation
-
A function
That is
- (Arnold 6.4.2) A necessary and sufficient condition for the direction field of the equation
to be a quasi-homogeneous is that the right-hand side be quasi-homogeneous and its quasi-homogeneous degree be
- (Arnold 6.5.1) Under a quasi-homogeneous dilation
- (Arnold 6.4.2) A necessary and sufficient condition for the direction field of the equation
-
A quasi-homogeneous vector field is defined by the condition