N-step Bootstrapping

• These methods act as intermediates in the spectrum between Monte Carlo (update at the end of the episode) and [Temporal Difference Learning|TD] (update immediately after),
• -step TD methods are those that update based on the temporal difference over steps.

Prediction §

• The return for an -step update is defined as

  For all and

• The n-step return is an approximation to the true return by truncating it after steps.

• We learn the state updates by using the following (simply substitute the n-step return for the formula in TD Prediction

• To compensate for the fact we do not perform updates at the first steps in the beginning, we make the updates at the end of the episode after termination and before starting the next episode.

• Like Monte Carlo, the n-step return can be written as a sum of TD errors.

¹

• The Error Reduction Property of -step returns means that the worst error of the expectation of an -step return is guaranteed to be a better estimate of than is.

  • This implies convergence to correct predictions as our n-step returns get progressively closer to the true value.

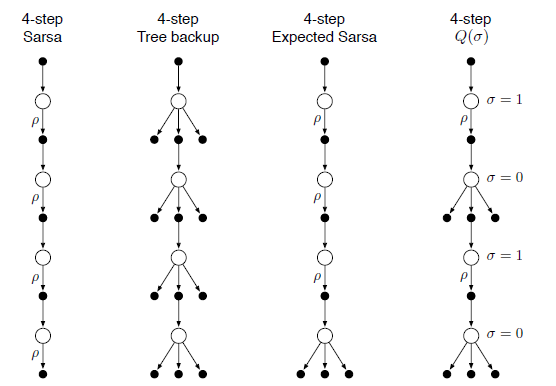
n-step SARSA §

• A generalization of SARSA.

• It still makes uses of sample transitions.

• We simply redefine the -step return to make use of .

  And if .

• The update rule becomes

• The value of other states remain unchanged. That is for all such that .

n-step Expected SARSA §

• It makes use o sample transitions, except for the last state which is fully branched.

• Extends -step SARSA as follows. We redefine the -step return as

  And if .

• We call the expected approximate value which is defined as

• If is a terminal state, then the expected approximate value is defined as .

-step Off-Policy Learning §

• We make use of the importance sampling ratio for n-step returns .

• The update rule then becomes weighted with as follows

• For using the Q function we use since we update on state-action pairs.

• For expected SARSA, we use . All possible actions are taken into account in the last state; the one actually taken has no effect and does not have to be corrected for.

• The drawback with off-policy methods is shown here — it requires slower training since it has higher variance updates.

Control Variates §

• One problem with importance sampling is high variance, especially when actions may not be taken
• We modify the definition of the return in this case to make use of an off-policy definition
  and where .
  • Here we remove the problem of high variance by having the target equal the estimate (i.e., do not change when ).
• For action values, we apply importance sampling to actions except the first.

  • Rationale: The first action is being evaluated and has already been taken, so the reward must be learnt in full.

  • The formula becomes

  • If , we have )

  • Otherwise, .

Tree Backup Algorithm §

• It makes use of all state transitions fully branched without sampling.

• In Tree-backup, updates are performed from the leaves of the tree. The actual actions taken do not participate.

• Each leaf contributes to the target with a weight proportional to its probability of occurring under target policy .

• Actions taken contribute to the probability of the leaves in the next level down.

• At the last node of the tree backup diagram, we consider all actions as untaken.

• We use the same one step return target as Expected SARSA. This form is generalized as follows

  For , .

• A special case: .

• The target is then used for the usual action-value update from n-step SARSA.

n-Step §

• Unifies n-step SARSA, Expected SARSA, and Tree Backup Algorithm by providing a choice. Either we fully branch or take samples based on some probability at time step .

  • If we fully branch all the time we get Tree Backup.
  • If we take samples, all the time we get SARSA.
  • If we take samples except for the last state we get Expected SARSA.

• may be a function on a state, action, or state-action pair at

• We use as an interpolator. The return is now defined as

  For .

  If , we end with .

  If , we end with .

• We then perform the update defined in n-step SARSA with control variates except without importance sampling ratios.

General N-step bootstrapping. Image taken from Sutton and Barto (2017)

Links §

• Sutton and Barto Ch. 7
  • 7.2 - n-step SARSA
  • 7.4 - Control Variates
  • 7.5 - Tree Backup
  • 7.6 - .

Footnotes §

1. Deriving this is a straightforward substitution, assuming the value function doesn’t change. ↩