-
A projective plane is a partial linear space where
- Any two lines meet at a unique point
- Any two points lie in a unique line.
- There are three pairwise non-collinear points (a triangle).
-
A projective plane is self-dual.
-
Let
be a partial linear space that contains a triangle. Then is a projective plane if and only if its incidence graph has diameter and girth . -
The incidence structure
is called the projective field plane and is described as follows: Points and lines correspond to -D and -D dimensional subspaces of vector space where . is incident with line if the subspace of is contained in the subspace of . - Each line contains
nonzero vectors. - Each point contains
nonzero vectors. - Each line contains
distinct points. - The entire projective plane contains
points. - The projective plane contains
linens with lines passing through each point. - It is easy to show that
is a projective plane - The corresponding incidence graph is
-arc transitive and also distance transitive.
-
Let
be a vector space over field with order . The projective space is a system of 1,2, and 3 dimensional subspaces of referred to as points lines and planes. - Each
-dimensional subspace contains nonzero vectors. - There are
totally isotropic points. - There are
totally isotropic lines. - Each totally isotropic point is contained in
totally isotropic lines
- Each
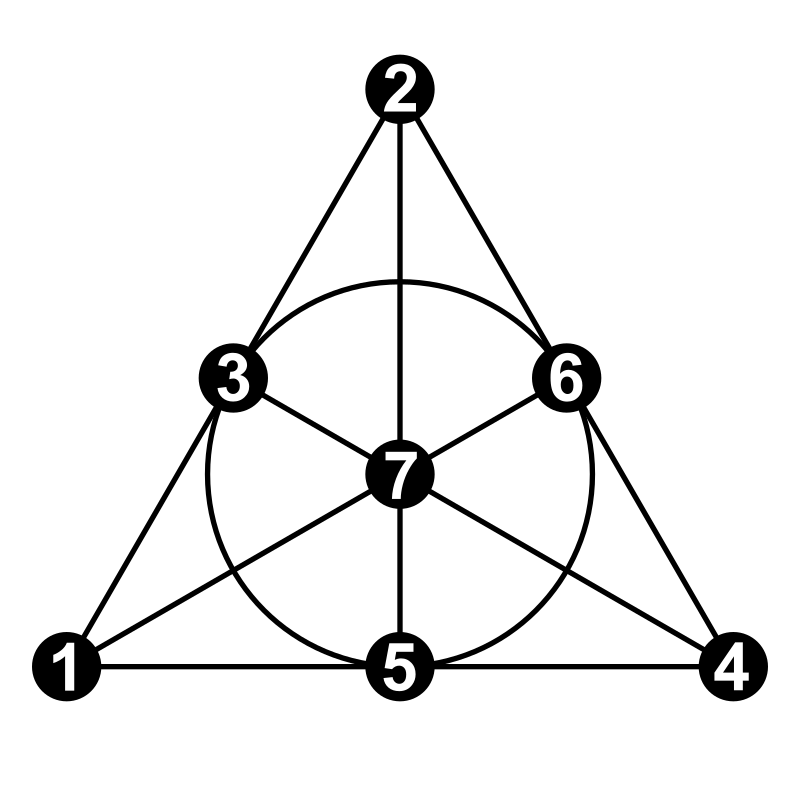
Fano Plane
-
The Fano Plane is a projective plane
-
It is a
design. -
It is a Steiner triple system
-
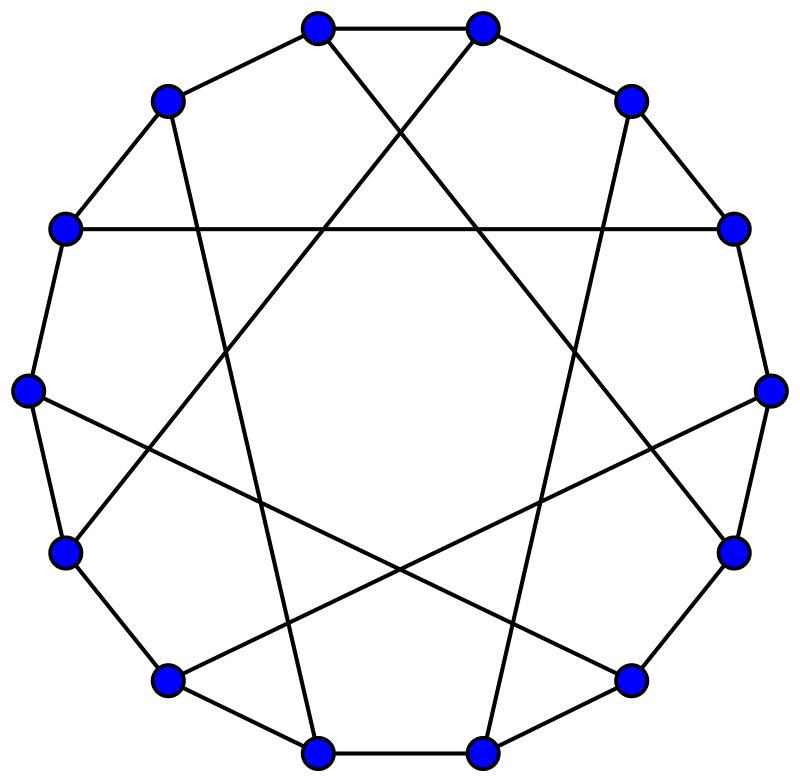
The incidence graph of the Fano plane is the Heawood graph