Graph View

Backlinks

The Library

Search

SearchSearch

Linear ODE

Jan 06, 2025, 5 min read

  • A first order homogeneous linear equation is an equation of the form

    This is a special case of an equation with separable variables.

  • (Arnold 3.1.1) Every solution to a first order homogeneous linear equation can be extended to the entire interval on which is defined. The solution with initial conditions is given as

  • The set of all solutions to a first order homogeneous linear equation form a vector space.

  • Homogeneous Linear Equations approximate any ODE by virtue of smooth functions being locally linear.

  • Integral curves map into one another under the action of dilation along the -axis in the extended phase space.

  • A first order homogeneous linear equation with -periodic coefficient is defined as an equation of the form

    Where

    • We can define a monodromy — a mapping such that we map the value to the value of the same solution for .

    • Intuition: We get a homogeneous linear equation with -periodic coefficient when we study the case of limit cycles.

      The linearity comes a monodromy which “unwraps” the limit cycle and maps it onto the real number line. Since it is cyclic it is periodic with period . Movement along the limit cycle can be encapsulated using the linear ODE above, hence linearity.

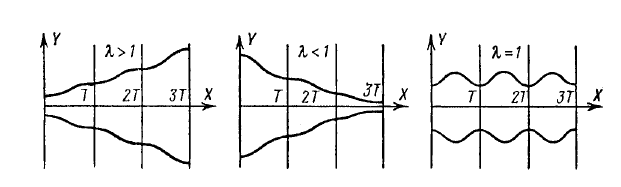
    • (Arnold 3.2.1) The monodromy operator is linear and is actually multiplication by a number . The behavior of solutions is determined by

      In particular, note that for integral curve , we have

      For , and serving as the translation term.

    • The multiplier term is obtained as

    • The multiplier characterizes the stability of a limit cycle.

      Missing \end{cases}\begin{cases}
    \lambda > 1 & \text{ limit cycle is unstable. Phase curves near a cycle diverge}\\

    \lambda = 1 & \text{ cannot be determined} \\
\lambda < 1 & \text{ limit cycle is stable. Phase curves near a cycle wind on the cycle}
\end{cases}
 $$
 In other words, if $\lambda = 1$, we cannot make judgments about the behavior of limit cycles
  * *Intuition*: Consider the function $\Phi$ such that $\Phi(\varphi(0)) = \varphi(T)$. When linearized, this function can be shown to be a monodromy. Intuitively, this maps one cycle (from $0$ to $T$, say) to another limit cycle. Thus, we can see how much the cycle diverges or stabilizes since $\Phi$ is a monodromy.

Monodromy. Image taken from Arnold

  • A first order Inhomogeneous Linear Equation is of the form

    • (Arnold 3.3.1) If a particular solution of an inhomogeneous equation is known, all other solutions have the form
      Where is the solution to the corresponding homogeneous equation (i.e., ). All such solutions are of this form.
      • Proof: See Friedberg 3.9. Note how the solutions to the homogeneous system forms a vector space (a null space in fact).
    • (Arnold 3.3.2) The solution of the inhomogeneous linear equation with initial condition exists, is unique, and is given by
    • Inhomogeneity typically corresponds to some form of perturbation on the system.

  • Superposition Principle If and are solutions of the inhomogeneous linear equations and then is a solution of the equation

    • We can separate the effects of different dynamics (the ’s). when taking into account all possible dynamics.

  • The solution of the equation

    Where is the Dirac Delta function.

    With initial condition is the influence function of the perturbation at the instant on the solution at instant .

    We also call this Green’s Function denoted

    • (Arnold 3.4.1) Green’s function is given by
      • For , any inhomogeneity disappears. For , the solution coincides with some homogeneous solution.
      • The above corresponds to the solution to a homogeneous equation with initial condition .
    • (Arnold 3.4.2) The solution of the inhomogeneous equation with inhomogeneity and with zero initial condition is expressed in terms of the influence function by the formula
      For .

  • (Arnold 3.5.1) If the solution

    With RHS of period in is such that the mean value of over a period is nonzero, then the equation has a solution of period , and exactly one solution.

    The solution is stable if the average value is negative It is unstable if it is positive.

    • Such a solution is inhomogeneous and of the form
      Where is the monodromy multiplier.
    • If then after a transitory process, the system has an oscillatory behavior. The oscillations are maintained by the perturbations to the system (i.e., inhomogeneity ).

Links