Heap Data Structure

• A min/max-heap is a data structure that obeys the min-heap property — the key of a node is greater than or equal to / less than or equal to the key of its parent.

Mergeable Heap §

• A mergeable heap is any data structure that supports the following operations

  • MAKE_HEAP - create and return a heap with no element
  • INSERT inserts an element whose key has already been filled in, into heap .
  • MINIMUM returns the pointer to the element in whose key is minimum
  • EXTRACT-MIN - delete the minimum element and return a pointer to it.
  • UNION - return a new heap that contains all the elements of the input heaps. Both input heaps are destroyed.

• Mergeable heap operations are lazy and defer work as late as possible.

Fibonacci Heap §

• A Fibonacci Heap also supports the following

  • DECREASE_KEY assigns to element within heap the new key value which is no greater than the current key value.
  • DELETE deletes element from heap .

• More formally, a Fibonacci heap is a collection of rooted Trees where each tree obeys the min-heap property.

  • All nodes in the tree are, ideally, linked together in a circular, doubly linked list.
  • All nodes keep track of their degree and whether or not they are marked. A node is marked if it lost a child since the last time they were made the child of another node.
  • The roots of all trees in a Fibonacci heap are linked together into a circular doubly linked list referred to as the root list

• Fibonacci heaps have good amortized asymptotic time bounds. MAKE_HEAP, INSERT, MINIMUM, UNION, and DECREASE_KEY take time. The other operations take .

  • The asymptotic bounds are dependent on the maximum degree .

  • If we only use the regular mergeable heap operations, we have that .

    If we include DECREASE_KEY and DELETE, we have .

• Fibonacci heaps are desirable when we rarely DELETE or EXTRACT-MIN. In practice, however, the complexity they have make them less desirable than ordinary heaps.

• The MINIMUM is found by maintaining a pointer to the root containing the minimum key. This pointer is updated during other operations

• The MERGE operation concatenates the root lists of two heaps together, and sets the MINIMUM as the smaller of the two heaps.

• The INSERT operation involves a node being appended to the root list.

• DELETE_MIN works in three phases.

  • The root containing the minimum element is removed and each of its children becomes a new root.

  • There may be up to roots. Successively link roots of the same degree while maintaining the min-heap property (make the one with the larger key the child of the other). Repeat until all nodes have a different degree.

    Use an array of length which maintains a list of pointers to one root of each degree.

    Link two roots if they have the same degree.

  • Update the MINIMUM accordingly.

• DECREASE_KEY works using cascading cuts.

  • First, if decreasing a key violates the min-heap property, cut it from the parent and update the minimum pointer if needed.
  • Start from the parent of . As long as the current node is marked, cut it from the parent and make an unmarked root.
  • Stop when we reach an unmarked node . If is not a root, it is marked.

• (CLRS 19.1) Let be any node in a Fibonacci heap, and suppose . Let be the children of in the order they were linked. Then and for . 7.

• (CLRS 19.4) Let be any node in a Fibonacci heap and . Then where is the -th Fibonacci number and is the golden ratio

van Emde Boas Tree §

• Supports the set operations of heaps in time provided that the keys are integers in the range with no duplicates, where denotes the size of the universe.

• We make use of a summary array structure to store whether or not an array contains a particular key. The summary array contains a of and only if the subarray contains a

• The key idea is to recursively use the summary array structure such that a new summary array encodes the one at the previous level of recursion. At the -th level the size of the universe is

  • The arises because we start with needing bits to encode the first summary array. Then at each level we reduce this number by half.

• More formally, the van Emde Boas tree or vEB tree for a universe of size is denoted .

  • If , then it is the base size and we can store an array of two bits.
  • Otherwise, in addition to the universe size , the data structure contains
    • A summary array structure which is a tree. It keeps track of which children are non-empty.
    • An array cluster of pointers, each to a structure.

van Emde Boas Tree. Image taken from CLRS

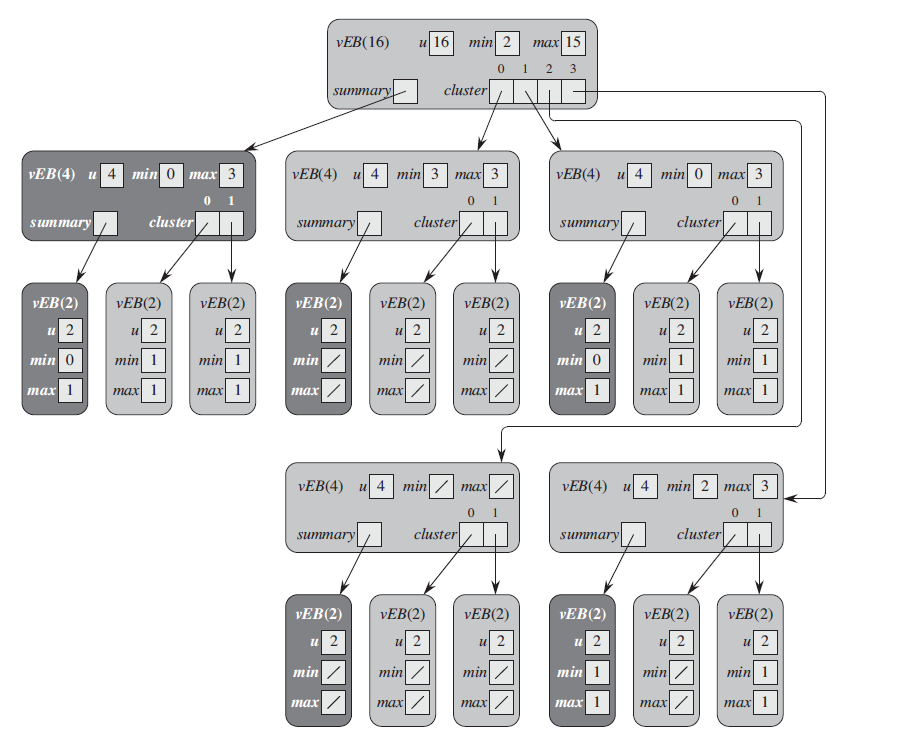
• Data is stored as follows.

  • The smallest and largest values are stored in T.min and T.max respectively.
  • Any value is stored in the subtree T.children[i], where .

• van Emde Boas Trees do not have optimal memory. For an bit integer, it requires bits of storage.

Links §

• CLRS - Ch. 19, 20